4. Generalizations.4.1 Figures of constant width in many directions.Instead of row, columns and diagonals, we now look for figures of constant width along a predetermined set of directions. Here I'll briefly sketch their construction. A direction
of the chessboard is determined by a vector
d=(a,b) in 

Definition. A figure of constant width w along the set of directions D is one such that every line with direction d in D intersects the figure in exactly w squares. In order to build figures of constant width on a given set of directions I'll make use of the notions of composition of figures and of extended constant width . The reader is referred to [Her-Rob] and [Riv-Var-Zimm] for the definitions. The following proposition is easily verified.
Proposition 1. If A has constant width v along d and B has extended constant width w along d then A composed with B has constant width vw along d.
Let D be a given set of directions.
For d in D
let F(d) be the figure
{kd, k=0,1,2,...,w-1}. Suppose that d is in the first
quadrant
of 
4.2 Figures of constant width on a toroidal chessboard.There is a simple arithmetical obstruction to having a solution of the n-queens problem on an nxn toroidal chessboard. Namely, n must be relatively prime to 6. In the same way, a figure of type (n,k,w) in an nXn toroidal chessboard... 4.3 Figures of constant width on an n-dimentional chessboard.? References.[Riv-Var-Zimm] I. Rivin, I. Vardi, P. Zimmermann, "The n-queens problem", Amer. Math. Monthly 101 (1994) 629--639. |
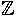 x
x