Chapter 6: Resistance to Extinction⁽¹⁾

Overview: In the three major sections of this chapter, we examine the findings and theories having to do with extinction and partial reinforcement. We start in the first section with an overview of extinction and related findings and procedures, and examine some factors that influence how rapidly extinction occurs. Three classical accounts of extinction are then presented. These include Hull's Drive Reduction Theory of extinction which claims that extinction involves a drive component, Guthrie's Contiguity Theory of extinction in which response competition plays the major role, and finally, the Mowrer and Jones claim (Discrimination Theory) that extinction involves learning to discriminate a current no-outcome situation from the previous response-generated outcome context the organism found itself in. The second section overviews the partial reinforcement effect. Various partial reinforcement schedules are discussed here, as are two popular theories of extinction following partial reinforcement: the Frustration Hypothesis of Amsel, and the Sequential Hypothesis of Capaldi. The final section presents and evaluates the work of people like Hulse demonstrating that animals are sensitive to global patterns of outcomes.

I. Acquisition of Extinction

        In short, extinction isn't the opposite of learning, it is learning. And the fact that it often seems to involve withholding a response should not mislead you about that. To remind you, performance is not the same as learning: What you see (or don't see, in this case) isn't all there is; there are numerous possible internal mechanisms and reasons behind the actual observed performance.
 

A. Preliminaries: Procedure & Relevant Findings

Some Basic Findings

        There are a number of factors that can influence resistance to extinction (and we will examine some of these below). But in general, extinction displays the same type of diminishing returns curve as does acquisition: The bigger changes will occur early in extinction, and later sessions of extinction will display progressively smaller changes in the response. Thus, as was true of acquisition, extinction involves a response being driven towards an asymptotic level of performance.

        Moreover, as you may remember, extinction is also characterized by a phenomenon referred to as spontaneous recovery: Presentation of the stimulus following extinction will likely cause momentary and temporary recovery of the response. How much recovery occurs will depend on several factors. One of these is the time interval between the last session of extinction, and the current test of the stimulus: The longer you wait after extinction to test for spontaneous recovery, the more likely it is that you will obtain it. Another is the number of sessions of extinction: With repeated sessions that take the animal close to the extinction asymptote, spontaneous recovery becomes less likely.

        As was true of acquisition, extinction is characterized by generalization: A response extinguished in the presence of one stimulus tends not to be observed in the presence of other, similar stimuli. (Of course, we assume here that the response was previously given to these, so that we are now seeing something new.) In this case, the resulting gradient is normally referred to as a gradient of inhibition.

        Finally, following extinction, relearning of the response will typically exhibit a significant savings score, consistent with the claim that extinction isn't simple forgetting. Indeed, theorists such as Rescorla have taken the speeded relearning as evidence that extinction doesn't technically involve replacing a response's excitation with inhibition. The argument Rescorla uses is that a truly inhibited response should pass the retardation test. That means that it should take longer to learn, resulting in a negative savings score. Thus, Rescorla views positive savings as evidence that extinction does not really involve inhibition (as was originally claimed by theorists such as Pavlov). But because there is a savings, we may at the same time presume that something of the original excitatory association has remained in the animal's memory.

        But what of the speed of extinction? Is there anything that might usefully be said about that? In fact, there is. As you already know from previous chapters, a number of factors influence the speed of extinction (its resistance). Thus, we read earlier (Chapters 4 and 5) about the Fowler and Miller and the Baum studies in which forcing competing responses speeded up extinction. We also read in Chapter 4 about the Boe and Church study in which punishment of the response during a pre-extinction 15-minute session speeded up extinction, the speed-up depending on the severity of the punisher. In Chapter 5, the Seward and Levy study on latent extinction was introduced, a study that will prove particularly relevant to evaluating several of the theories below. To remind you, Seward and Levy associated a goal box with non-reinforcement, and found that this speeded up extinction of running to the goal box. And finally, the partial reinforcement effect was briefly discussed in Chapter 4. In partial reinforcement schedules, only some responses are reinforced during learning, rather than every single response. Different partial reinforcement schedules will have differing effects of extinction, but in general, partial reinforcement will lead to greater resistance to extinction than continuous reinforcement.

        One final preliminary is worth noting here: With continuous reinforcement, whatever tends to result in faster acquisition or a higher rate of acquisition during learning will, paradoxically, result in faster extinction. Both Roberts and Amsel, for example, have shown that larger reinforcers lead to faster extinction when they are removed. In like fashion, there are a number of studies suggesting that greater numbers of continuously reinforced trials during acquisition will result in faster extinction. Such findings are at first blush problematic for associationist theories that claim that larger reinforcers or more pairings result in a stronger association: Shouldn't a stronger association result in longer-lasting learning?

Alternative Procedures

        There are actually a number of procedures that may be used to lower the expression of a response. One that you are certainly aware of, for example, is punishment training: the association of a response with an unpleasant outcome. Although extinction and punishment at first seem different, there are some strong similarities between them at an abstract level, especially when we are dealing with the extinction of a previously-reinforced response. In some sense, we can think of extinction in this situation as the removal of an expected reinforcer following a response, and that definition gets us very close to the definition of negative punishment that we briefly considered in Chapter 4. On this account, the normal extinction procedure represents a kind of mild punishment. Of course, we learned earlier in the Boe and Church study that mild punishers do not work well. However, if you go back to that study, you will see that mild punishers are as effective as extinction: They work more slowly than strong punishers, but they eventually do work. In many studies in which mild punishers have seemed ineffective, they have failed to be compared to extinction. Perhaps the temporary suppression of behavior by a mild punisher ought more properly to be compared to the temporary suppression in extinction. In the latter, as you know from our discussion of spontaneous recovery, there is also a recovery of the response, the amount of recovery depending on the amount of time that has passed.

        The point of this discussion, of course, is to broaden our horizons about how to think of extinction. If we regard extinction as the loss of an expected outcome, then there are really a number of procedures that may fit this definition in addition to punishment training and simple loss of the outcome. We can add to our list omission training, for example, in which we typically require an animal to withhold a response that has previously been associated with reinforcement. In the typical omission training procedure, unlike the two procedures mentioned above, we actually now reinforce the animal for not responding. An example is the Sheffield experiment described in Chapter 4, in which dogs were rewarded for not immediately drooling in the presence of food.

        Another procedure we came across in the last chapter (in the discussion on Premack) was to follow a strong response (a preferred response) with a weaker (less preferred) response. That procedure by itself doesn't easily fit the portrait of extinction we are starting to build up. But if you now re-analyze this situation from the point of view of Timberlake and Allison's response deprivation hypothesis (the equilibrium theory), you can see that this procedure deliberately throws the weak response out of equilibrium: The procedure moves the weak response well above its bliss point. Having a response out of equilibrium is a type of punisher, so that we would now expect the animal to moderate the expression of the stronger response down, in order to find the best compromise for how often these two responses are performed (i.e., the point nearest their joint bliss point). Indeed, you may wish to consider what the Timberlake and Allison theory might have to say about following a response with a punishment such as shock. Shock certainly has to be an activity that occurs well above its bliss point in this type of experiment, resulting in strong pressure to moderate the shocks downward. Thus, certain types of experimentally induced disequilibrium can result in smaller levels of responding.

        A final procedure that we can discuss here involves simply removing the contingency between the response and the outcome. That is, we move the animal to some point on the diagonal in the optimal contingency space. On the diagonal, the probability of an outcome is the same whether the animal makes or withholds the response, resulting in a zero contingency between the response and the outcome. To remind you, Hammond found that rats that had learned a response ceased making the response once the contingency became zero. Normally, procedures such as omission training and establishment of a zero contingency result in a slower build-up of non-responding compared to the typical extinction procedure, but over the long haul, they appear to be as effective as extinction.

        Now that we have discussed some of the preliminaries, let's move on to some of the classic theories of extinction.
 

B. Hull: Extinction & Drive Reduction

Formulation Of The Theory

        Let us start with the notion of two associations, one excitatory; the other, inhibitory. The excitatory association is _SH_R, of course, the habit strength between a stimulus and a response. The inhibitory association, by contrast, is _SI_R, which Hull termed conditioned inhibition. At the start of learning (and generally, until after the extinction procedure has started), _SI_R is at zero.

        But you will recall that there were two types of inhibition in Hull's system. The other type of inhibition was not learned. This type Hull called reactive inhibition, or I_R. Do note that there is no subscript for the stimulus in the formalism for reactive inhibition. That is because reactive inhibition doesn't depend on the stimulus at all. Rather, reactive inhibition is a type of fatigue or resistance that occurs with the performance of a response, and that makes that response a little bit less likely to occur in the immediate future. Normally, during initial learning, the presence of a reinforcer increases the habit strength, so that we get boosts in both _SH_R and I_R. But the bigger boost presumably occurs in _SH_R, which means that excitation will be larger than inhibition. So long as that is the case, we would expect to see continued responding during learning, even though we may presume that there is a lot of reactive inhibition about, if the learning trials are spaced relatively closely together.

        Fatigue, however, is something that we recover from by resting. In like fashion, Hull claimed that reactive inhibition would fade away when the animal had a chance to rest from doing the response. So, in any given situation, the amount of reactive inhibition would depend on how long ago the animal had responded.

        That brings us to the normal extinction procedure, in which we remove the reinforcer. Once the reinforcer is gone, _SH_R no longer increases. But as the animal keeps responding, reactive inhibition keeps increasing, until finally, the total amount of reactive inhibition exceeds the amount of excitation. And when that happens, by the principle of algebraic summation (i.e., effective reaction potential), the animal ceases to respond.

        There is a sense in which this should remind you of the approach-avoidance situation we discussed earlier. Like Hull, Dollard and Miller claim that a response can be associated with both excitation and inhibition. And like Hull, they claim that whether the animal makes or withholds the response (runs towards or away from the goal in the example from Dollard and Miller in Chapter 4) depends on algebraic summation. But unlike Hull, their avoidance gradients (inhibition) don't change with rest.

        An illustration might be useful at this point. Figure 1 shows some sample results that represent what might happen at various stages during extinction. In each case, the light blue bars (the ones with the letters in them) represent the habit strength, or _SH_R . These bars are identical to one another: They represent how strong the habit strength is, going into extinction. Because there is no more reinforcement, the habit strength will not change.

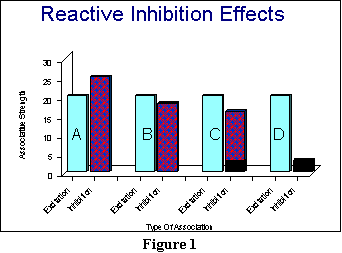        The first two bars (the A pair) are meant to capture roughly what happens well into extinction, at a point where the reactive inhibition has built up dramatically. (Reactive inhibition in Figure 1 is represented by the patterned bars: the purple bars, for those of you with a color monitor.) In this case, the reactive inhibition has increased past the level of excitation. Now assuming (for the sake of argument) that D and V and K are all equal to 1, then the animal should no longer respond at this point: Inhibition should be greater than excitation, so that there will be a negative effective reaction potential.

        However, since the animal at Point A stops doing the response (and starts resting those muscles associated with that particular response), the reaction inhibition now has a chance to start fading away. Thus, after a relatively short while, reaction inhibition will decrease to the point that inhibition is now slightly less than excitation. That point is represented by the B bars (the second pair of bars) in Figure 1. Note that excitation is stronger, so we would expect the animal to start responding again (because the effective reaction potential in this example has now gone positive).

        One more point is important about what happens at B: Hull considers reactive inhibition to be an unpleasant drive state. And as you can see in comparing what happens to inhibition at Points A and B, there is drive reduction. Thus, we have met the condition that there be some sort of reinforcer present for learning during extinction. That reinforcer is the decrease in reactive inhibition over time. But note that this decrease occurred because the animal performed a response that allowed the reduction in reactive inhibition. What was that response? Quite simply, the response of not using the particular muscle movements it had been executing earlier. We will call this the response of not responding, for short. Thus, at Point B, the animal is reinforced for not responding, because the reactive inhibition has lessened a sufficient amount.

        The response of not responding is what Hull has in mind when he speaks of conditioned inhibition. Please understand that this conditioned inhibition is not a drive state, unlike the reactive inhibition. Instead, it is a learned association between the stimulus and a response that essentially teaches the animal not to do that response. Thus, a little bit later, at Point C, the total inhibition the animal will have can be represented by the amount of reactive inhibition it still has left, and by the amount of conditioned inhibition it has now acquired. I have represented conditioned inhibition with the dark region of the inhibition bar in C. As you can see, there is a bit of conditioned inhibition here, but much more reactive inhibition. However, since the total inhibition is less than the excitation, we would expect the animal to start responding again at Point C. If, however, we have removed the animal from the experimental apparatus so that it cannot make the response, then with additional time (and rest), the reactive inhibition should have totally dissipated, leaving only the conditioned inhibition behind. This situation is represented by the D pair of bars. At Point D, there is a great deal of excitation, and some conditioned inhibition. Thus, when we decide to return our animal to the apparatus, the animal should start the process of (futilely) making the response anew. Like excitation, conditioned inhibition can never decrease.

        You can work out from this example what should happen next. The animal keeps responding until reactive inhibition builds up so that total inhibition (reactive and conditioned) exceeds excitation. Of course, less reactive inhibition will be needed for a negative effective reaction potential than previously, because there is some conditioned inhibition present. In any case, when the inhibition builds up to sufficiently high levels, the animal stops responding. That results in a further opportunity for drive reduction, which, in turn, increases the total amount of permanent, conditioned inhibition. This cycle continues until conditioned inhibition is always higher than excitation. At that point, extinction has been successfully completed.

Some Compatible Predictions

        There are a number of findings that are compatible with this approach to extinction. Some of these we have discussed previously. Among these is the spacing effect. To remind you, the spacing effect refers to whether initial learning involves massed practice in which there is very little break between trials, or spaced practice in which the animal rests a bit before going on to the next trial. All other things being equal, spaced practice results in significantly better learning.

        You can probably figure out why Hull's model is compatible with this approach. Reactive inhibition should occur each time the animal responds in either condition. But in spaced practice, there is time for the reactive inhibition to decrease between trials. So, by algebraic summation, there should be relatively more net excitation in spaced practice, resulting in a stronger response.

        There is another finding arising from the spacing effect that also fits this model. For this finding, we will restrict ourselves to a condition in which we put our animals through just massed practice. Following the end of the practice session, there is a tendency for the response to get stronger with time. The diagram for this experiment would be something like the following:

            Group         Initial Learning                     Response Tested At

            1                massed practice                     5 sec after practice
            2                massed practice                     30 min after practice

Here, Group 2 will show a stronger response, even though both groups have had the same initial learning. This finding is called the reminiscence effect. The reason it fits Hull is that Group 2 has had an additional 30 minutes in which to allow reactive inhibition to go away. So, its relative excitation (effective reaction potential: excitation minus inhibition) will be stronger.

        A second compatible finding is spontaneous recovery. If you go back to Figure 1, you can see why spontaneous recovery should occur by comparing relative excitation at Points A and B. At Point B, the reactive inhibition has decreased past the excitation, so that the response is now positively excited once more. In general, when we think we are at extinction, there is a little bit of reactive inhibition on top of a large amount of conditioned inhibition, and when that little bit of reactive inhibition goes away, the conditioned inhibition may be below the conditioned excitation. To give you a feel for this, spontaneous recovery reaches a maximum several hours after extinction, and may then persist for several days. Indeed, Mackintosh and others have found that the amount of spontaneous recovery can be quite substantial (see also a recent interesting simulation of this effect by Dragoi and Staddon).

        Of course, it is possible to get rid of spontaneous recovery, but the procedure that is normally required involves successive sessions of extinction. If you think about what goes on in successive sessions, you will realize that each session builds up more and more conditioned inhibition, so that each succeeding session will require less and less reactive inhibition before the animal stops responding. Our prediction here is that spontaneous recovery should decrease over repeated sessions (it does!) until, finally, there is no spontaneous recovery because conditioned inhibition always equals or exceeds excitation.

        A third set of findings involves the effort or strength required to make a response: The more effort is required, the faster the extinction will be. From the standpoint of Hull's theory, greater effort will fatigue the muscles more, resulting in greater reactive inhibition.

        One more compatible finding may be mentioned. If we compare the normal extinction procedure with the procedure of moving the animal to a zero contingency (as in Hammond's study), we find initially slower extinction in the latter. This is also consistent with Hull, at least at broad scale: A zero contingency means that there will be some random pairings of a response with drive reduction. Thus, conditioned excitation no longer stays at the same level in this procedure. If excitation is rising along with inhibition, then we would certainly expect extinction to slow down compared to the usual procedure.

Incompatible Findings

        I earlier wrote that the Seward and Levy study would prove important for evaluating a number of theories. Here is our first test case. They set up their experiment as follows:

            Group                 Phase 1                 Phase 2                     Phase 3

            Experimental     run to goal            in goal with no RF     extinction
            Control               run to goal                                               extinction

And what they found, of course, was that the group with the experience of being placed in a goal box that no longer delivered food extinguished more rapidly. Apparently, their process of extinction had already started in Phase 2.

        So why is this finding problematic for Hull? The answer will turn out to be quite similar to the reason Light and Gantt's finding (the study on classically conditioning paw withdrawal in temporarily paralyzed dogs) was problematic for Hull's theory of classical conditioning. For Hull, a response has to be made in order for learning to occur. And specifically with respect to extinction, a response has to be made in order for there to be a build-up of reactive inhibition. But the animals in Seward and Levy's experimental group did not make the response of running to the goal box. Therefore, that response could not have become associated with I_R.

        A similar type of finding occurs in a study by Heyes, Jaldow, and Dawson. They did an experiment on observational learning in which one group of rats saw another go through extinction (i.e., our group saw the others perform a response they had also learned, but they also saw that the response longer resulted in reinforcement). As you might expect from the discussion of vicarious punishment in the previous chapter, the observational group exhibited faster extinction. But as in the Seward and Levy study, the observational group had apparently started the process of extinction before ever making a non-reinforced response. They should not have had any reactive inhibition from simply observing other rats. Hull would therefore have a great deal of difficulty explaining this finding. As you may imagine, there are now a number of studies that employ some variant of a procedure in which extinction can commence in the absence of an overt, physical, non-reinforced response by the animal.

        A third class of findings concerns the partial reinforcement effect. Normally, animals on partial reinforcement exhibit slower extinction. However, Hull would predict the exact opposite finding, as continuously reinforced animals have had more trials involving drive reduction, and thus, should have a much stronger habit strength.

        Finally, a related problem for Hull involves the fact that extinction in continuously reinforced animals appears to be inversely related to the number of acquisition trials. For Hull, having a large number of reinforced trials should mean having very strong habit strength, so that a very high level of inhibition will be needed before the animal stops responding (i.e., before the inhibition equals or exceeds excitation). However, quite the opposite effect tends to occur: Large numbers of continuously reinforced trials appear to result in faster extinction rather than the predicted slower pace.

        You already know of the numerous problems that Hull's theory of excitatory learning ran in to; those problems combined with the issues mentioned above were sufficient to send theorists scurrying for another explanation.
 

C. Guthrie: Extinction & Response Competition

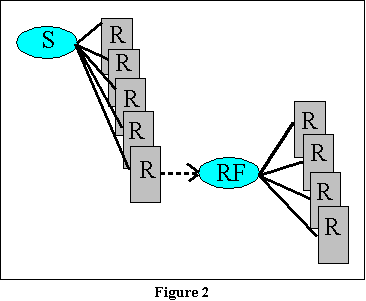        In any case, once the response we are interested in is emitted by the animal, a new stimulus (the reinforcer indicated by the second oval) enters into the context. And as you can see from this diagram, the responses that condition to this new stimulus do not overlay the previous response that led to it (bar pressing, for example).

        So, there is nothing magic about reinforcement in Guthrie's theory. Indeed, any significant stimulus that causes the animal to orient to it should have had the same effect, and not just those stimuli that involve food or drink.

        Given this, Guthrie's theory of extinction is simply as follows: When a given response no longer leads to reinforcement, other responses may now be made after it that will overlay (and thus compete with) it. Accordingly, the principle of postremity will now support the expression of the later responses. Thus, much as did Hull, Guthrie believes that extinction is also learning. But, it is the learning of new responses that will compete with the old response. Remove the second oval in Figure 2, and you now have the opportunity for a very long deck of responses in which bar pressing is somewhere in the middle, instead of on top.

        The principle of response competition is an important one, although many theorists feel that response competition needs to be associated with further mechanisms such as frustration (see the discussion of Amsel's theory below). Nevertheless, there are a number of studies that support the idea that competing responses will speed extinction. We have already briefly read about the Baum and the Fowler and Miller studies at the beginning of this chapter. To remind you, Baum looked at the course of extinction of an avoidance response. In one experiment by Lenderhendler and Baum, rats were flooded with danger signals during extinction, because they were physically prevented from leaving the area where they had previously been punished. In this situation, as you may remember from our discussion of learned helplessness, they tend to freeze after a few seconds. Freezing, of course, isn't a competing response, as Maier demonstrated: It is an SSDR to a danger signal. But what Lenderhendler and Maier did was to force the rats to move around a bit by pushing them. That act should result in competing responses being emitted, since it forces a variety of behavioral responses out of the animals. Consistent with Guthrie's theory, rats forced to move displayed faster extinction.

        Similarly, in the Fowler and Miller study, rats entering a goal box were shocked either on their front paws, or on their rear paws. Shock at the rear causes forward movement which is compatible with the response of moving forward to the goal; shock at the front causes backward movement which is the opposite of the response of moving forward. Note in this experiment that both groups of animals are receiving the same shocks, and that both groups of animals could have avoided these shocks simply by refusing to enter into the goal area. Nevertheless, the results were consistent with the principle of competing responses: The front-shock group extinguished more rapidly.

        An experiment by Adelman and Maatsch also well illustrates the effect of response compatibility. In their study, rats were trained to run to a goal box, as in the Fowler and Miller study. However, during extinction, one group of rats had to go back into the alley to be removed from the maze, whereas a second group had to jump over a hurdle from the goal box into a further portion of the maze to be removed. Much as in the Fowler and Miller study, one group thus performed responses that were incompatible with the original response (going back versus going forward), but the other performed responses that were compatible (both involving going forward). As you ought by now to expect, the group that had to continue going forward took longer to extinguish.

        From the latter two studies, in particular, we can derive an important point: Only some of the responses acquired later will be competing responses. It is possible for an animal to acquire a series of compatible responses that effectively maintain its performance because they include important components of the earlier response, or because they essentially constitute a minor modification or elaboration of the earlier response, or because they may be expressed simultaneously with the original response.

        Despite the successes of competing response theory, however, there are also indications that additional factors will need to come into play. Scavio, for example, trained rabbits with the nictitating membrane paradigm in classical conditioning. The rabbits learned to blink to CS1 because CS1 had been paired with a mild shock administered near the eye. Later, Scavio found out that presence of CS1 interfered with rabbits learning to move their jaws to food in the presence of another CS. (This involves the summation test we learned about earlier.) The reason this poses a problem for Guthrie is that jaw movement and eye blinking are not competing responses: It is possible to do both at the same time. Of course, the shock UCS and the food UCS may involve very different, competing emotional states, but competing emotions were not what Guthrie's theory was about.

        A final point concerning Guthrie's theory is that the Seward and Levy study on latent extinction and the Heyes et al. study on observational learning are, strictly speaking, not completely compatible with Guthrie. Regarding the latter study, animals that are observing other animals go through extinction aren't really making competing responses (at least, any more than animals watching other animals go through acquisition), so that they ought not to have a headstart on extinction. (There is an interesting empirical question here that Bandura's theory suggests: Does vicarious punishment result in differential behaviors in the observing group while it observes? That is, can we build a theory in which watching others go through extinction increases our activity at that moment, so that new responses may be associated with the observable stimuli?) And regarding the Seward and Levy study, animals temporarily placed in a goal box without food might be acquiring competing responses having to do with the stimulus complex of being in the goal box, but no competing responses are being associated with the start box or the alley to the goal box, since the animals are not placed in that portion of the maze.

        The notion of competing responses is certainly important, but contrary to Guthrie, it is not the sole explanation of extinction.
 

D. Mowrer & Jones: Extinction & Discrimination

        Mowrer and Jones's theory, the Discrimination Hypothesis, is a good sample representative of this group. According to Mowrer and Jones, the animal in extinction essentially has to learn that this is a new stimulus condition for which a different response is appropriate. Put that way, the animal has to learn to discriminate between the learning stimuli and the extinction stimuli. However, one of the findings that we know from the literature on generalization and discrimination is that ease of discrimination between two stimuli will be inversely related to their similarity. Greater similarity results in greater generalization, which makes learning the discrimination more difficult. You can, if you wish, come up with a variety of reasons why similar stimuli ought to yield greater difficulties in discrimination learning (see also the next chapter). Perhaps they are simply much harder to tell apart, so that the animal has to spend additional time orienting to subtle differences between them. Alternatively, from a Hullian point of view, perhaps the greater generalization means a higher level of conditioned excitation that requires extended training to overcome (i.e., more trials to build up sufficiently high levels of conditioned inhibition). The precise reason for the finding is less important, at the moment, than the general principle that similarity will influence rate of extinction.

        An obvious test of the Discrimination Hypothesis is to vary the similarity of learning and extinction, in order to see whether greater differences lead to faster extinction. (Guthrie would make the same prediction, by the way; can you figure out why?) A good example of this type of study involves an experiment by Welker and McAuley. They trained four groups of rats to bar press in a Skinner box. All groups were trained in the same way, and the training involved both being transported to the experimental apparatus in the same fashion, and being surrounded by the same types of contextual cues once in the Skinner box. In terms of mode of transportation, the rats first had the water bottles removed from their home cages, and then had the cages placed on a trolley with a paper liner. In the Skinner box itself, there were wood shavings on the floor; a lighted circle above the bar; and a continual noise in the background.

        The four groups of rats were then put through extinction procedures, but their extinction procedures differed. Essentially, the design for extinction was as follows:

            Group         Extinction Procedure

                1             no more RF
                2             new transportation; no more RF
                3             new box cues; no more RF
                4             new transportation & box cues; no RF

        The new box cues involved the disappearance of the noise and the light, and the use of a paper liner at the bottom of the Skinner box rather than wood shavings. Similar changes were implemented having to do with the stimuli involved in the transportation method. Welker and McAuley found the fastest extinction for the groups with the new box cues (Groups 3 and 4), and the slowest extinction for the group that just had the reinforcer removed (Group 1). The group with the new method of transportation (Group 2) was in between these.

        There is a certain sense in which the Discrimination Hypothesis is similar to an important theory having to do with human memory. This is Tulving's Principle of Encoding Specificity (see Chapter 8). According to Tulving, when we form memory episodes, we also include information about the environmental cues that were present at the time of the event. Remembering in part involves using probes or retrieval cues that will prime or activate the appropriate memories (remember the discussion of Wagner's model of classical conditioning!) The best retrieval cues, of course, will be those that are actually part of the episode or memory. Thus, Tulving points out that memory ought to be most successful when we are in an environment similar to that in which we originally learned. The reason is that by looking around us at the environment, we should already be activating some of the environmental cues that were earlier included in the memory. So, there is a similarity principle here that states that similarity of learning and retrieval contexts will facilitate recall.

        Let us now coordinate this principle with the Discrimination Hypothesis. If the environment the animal finds itself in is completely different, then we would not expect any memories of a given response to be activated that would result in performance of that response. In this sense, there will be no need to learn to extinguish the response, because it is simply not elicited by the environment. But as the extinction environment becomes more similar to the original learning environment, the memories of what the animal did earlier are more likely to be primed. Extinction in this sense involves acquiring new memories that activate a different response. Thus, how strongly a given environment activates old memories of responding can be taken as a rough guide to how much interference there will be with learning a new response.

        We can perhaps capture the relationship between these two compatible approaches by stating that Tulving's theory has to do with how easy it is to remember in similar contexts, and Mowrer and Jones's theory has to do with how hard it is to suppress or overcome those memories in similar contexts.

        There is an important lesson here for you in Tulving's work. When you take an exam, try to reinstate the context in which you originally studied the materials. Thinking about that context or environment may help provide you with appropriate retrieval cues. We will see in a later chapter that this is a powerful technique, and you will learn about a number of studies that support it. In the meantime, it is a principle you can put to work.

            Back to Mowrer and Jones's theory: Note that this theory in principle can also explain the effects of large reinforcers during initial continuously reinforced learning (e.g., Roberts's finding that large reinforcers lead to faster extinction). A standard experiment on reinforcement size effects would involve a design such as the following:

            Group         Acquisition Phase             Extinction Phase

                1             small reinforcement         no reinforcement
                2             large reinforcement         no reinforcement

I have included this design because it makes obvious the change in similarity between the two groups in the acquisition and extinction phases. You need to think of a reinforcer as one of the stimulus elements that define the context in which responding is maintained. Within this framework, a small reinforcement is more like no reinforcement than a large reinforcement is. Our prediction from the Discrimination Hypothesis would thus be one of greater resistance to extinction in Group 1, precisely the result that Roberts and others obtain.

        As a final example of work compatible with this theory, we may consider a study by Dyal and Sytsma. They ran four groups of animals, three of whom had some exposure to partial reinforcement (recall that the partial reinforcement effect predicts greater resistance to extinction in partially reinforced groups). In all groups, there were two sessions of reinforcement-based learning, but two of these groups had a session of continuous reinforcement, and a session of partial reinforcement. These two differed in which came first. The issue Dyal and Sytsma looked at was whether order of the sessions would influence speed of extinction.

        Here is their design:

            Group         Session 1             Session 2             Session 3

                1             continuous RF     continuous RF     extinction
                2             partial RF            partial RF            extinction
                3             partial RF            continuous RF     extinction
                4             continuous RF     partial RF            extinction

        Note that Groups 3 and 4 have exactly the same amount of partial reinforcement during learning. If all that is important in the partial reinforcement effect is the number of partially reinforced trials, then we would predict that they ought to be identical, and show greater resistance to extinction than the continuously reinforced group (Group 1), though perhaps not as much resistance as the group with the most partial reinforcement (Group 2).

        Can you predict what happened, and why it fit the predictions of discrimination theory? First, the usual partial reinforcement effect did occur in the first two groups: Group 2 showed greater resistance to extinction than Group 1. Although we have not discussed this explicitly until now, that also fits the Discrimination Hypothesis, since partial reinforcement (in which there are some trials with no reinforcement) is more like extinction (in which all trials have no reinforcement) than continuous reinforcement is. And second, Group 4 had a stronger partial reinforcement effect than Group 3! You can see why this result would be expected from the Mowrer and Jones theory by comparing Sessions 2 and 3 in the design above: Group 3's Session 2 was reasonably different from their Session 3, making it reasonably easy to tell the two apart. However, Group 4's Session 2 was similar to their Session 3, making it harder to tell them apart. As this study clearly shows, there is more to the partial reinforcement effect than simply determining how many trials of partial reinforcement the animal had.

        As you can see, the Discrimination Hypothesis has a number of appealing features. It can account for reinforcement size effects, and more to the point, the partial reinforcement effect. It can handle other findings relating to extinction, as well. For example, animals who have been trained with delayed reinforcement have greater resistance to extinction. (One could argue that extinction involves a very, very long delay of reinforcement, so that increasing delays during learning make the acquisition phase more similar to the extinction phase). However, more specialized versions of the theory have been developed to account for a broader range of findings in partial reinforcement, and we turn to these next.
 

II. Extinction & Partial Reinforcement

A. Humphrey's Paradox: The Partial Reinforcement Effect

        One of the first psychologists to report the partial reinforcement effect was Humphrey, and it became known as Humphrey's paradox. It initially puzzled a number of theorists for the simple reason that everyone at the time believed that more pairings of a response with a reinforcer ought to result in a stronger, more lasting association. Thus, the paradox Humphrey discovered was that under certain circumstances, less was more: Fewer reinforcers could eventuate in an apparently more durable association.

        Although Pavlov did indeed look at partial reinforcement trials in his work, the status of partial reinforcement effects in classical conditioning today remains inconclusive. The results of studies in classical conditioning are contradictory, and it may be safest to conclude that partial reinforcement here (in which the CS is only sometimes paired with the UCS) has, at best, weak effects. Thus, partial reinforcement effects seem to constitute an area in which classical and operant conditioning tend to yield very different findings.

        Before we go on to specific theories and findings, one more point is worth mentioning: There are indeed reports of the occasional reverse partial reinforcement effect (or reverse PREE), in which partial reinforcement will actually cause faster extinction. There is an interesting article by Nevin that discusses this, and the upshot (although we will certainly see some exceptions below!) appears to be that a partial reinforcement effect is more likely when there have been a relatively large number of acquisition trials, but a reverse PREE becomes possible when there are only a small number of trials. You may wish to keep this finding in mind as you evaluate the theories and findings below.
 

B. Partial Reinforcement Schedules

Simple Schedules

        A number of simple schedules have been proposed, but most people really concentrate on four simple schedules. These four schedules may be defined in terms of two broad dimensions. The first dimension involves repetition. We can have a pattern of events that constantly recycles or repeats, in which case the schedule is referred to as a fixed schedule. Alternatively, we can have a random pattern in which there is no systematic repetition. The latter is referred to as a variable schedule. Note that fixed schedules in theory may be predictable (that is, the animal or human might be able to develop an expectancy concerning when a response will be reinforced), whereas variable schedules are, by definition, unpredictable. (Well, to be more accurate, they are not successfully predictable: Many people who play slot machines mistakenly think they can predict the machine's behavior!)

        The second dimension relevant to defining simple schedules involves what must happen for a response to be successful in obtaining an outcome. We can refer to this dimension as the response criterion. By criterion, I mean what has to happen before the response in order for it to work. In one set of schedules, the criterion or rule involves the number of responses that have gone on before. This involves a response-dependent rule: A certain number of responses, on average, has to occur before a reinforced response. This type of schedule is referred to as a ratio schedule. Alternatively, a criterion may involve a time-dependent rule: A certain amount of time, on average, has to pass before a response will work. Those types of rules involve interval schedules. When we combine these two dimensions in all possible combinations, we obtain the four simple schedules outlined in the table below:

            ________________________________________________________________

                                                                                Criterion
                                         _________________________________________________

            Repetition                 Response Dependent                 Time Dependent
            ________________________________________________________________

            Fixed                         fixed ratio schedule                 fixed interval schedule

            Variable                   variable ratio schedule            variable interval schedule
            ________________________________________________________________

        Let's discuss each of these schedules in more detail. The easiest of these to start with is the fixed ratio schedule (often abbreviated FR). In a fixed ratio schedule, the animal needs to perform a certain number of responses (the ratio) in order to get its reward. Actually, continuous reinforcement is a special case of a fixed ratio schedule, except that it is a fixed ratio 1 schedule (FR1), meaning that the animal needs to emit one response (the correct response, of course!) to get its reward. In like fashion, a pattern in which the animal has to make two responses to get a reinforcement is an FR2 schedule. The number following the FR tells you which response gets the reinforcement, and how many responses before that have gone unreinforced. Thus, in FR357, the 357^th response works, but the animal has had to make 356 earlier responses that did not lead to any reward. As you might imagine, the schedule becomes harder to learn as the number goes up. Typically, with very large ratios, we have to wean the animal towards the ratio; that is, we start with much smaller ratios, and slowly increase the number of non-reinforced trials.

        As a rule, higher ratios result in greater resistance to extinction. So, we would expect more resistance with an FR300 than an FR20 schedule, for example. Based on what you know about Mowrer and Jones's Discrimination Theory, you ought to be able to predict this result.

        There are many examples of fixed ratio schedules in the real world. In many book or CD clubs, for example, if you buy a certain number of books or CDs, then you get a free book or CD. Similarly, in a work environment, salary incentives based on sales could be considered an example of a fixed ratio: A bonus for every 5 sales concluded would be an FR5 ratio, for example. Piecemeal work also fits this category, when the salary depends on how many pieces are finished.

        In a variable ratio schedule (abbreviated VR), on the other hand, the precise response that will obtain the reinforcer is not easily predictable. Rather, there will be a certain average number of responses that have to be made. So, a VR3 schedule means that, on average, 1 out of 3 responses will work, though it won't be every third response, as it would have been in the FR3 schedule. Variable ratio and fixed ratio schedules that have the same number will have the same overall density of reinforcement: They will have the same numbers of reinforced and non-reinforced responses, but not at the same places. Thus, below are a sample FR3 and VR3 schedule (in which the R and N stand for reinforced and non-reinforced responses, respectively):

                FR3:         N     N     R     N     N     R     N     N     R     N     N     R
                VR3:         R     N     N     N     R     R     N     R     N     N     N     N

If you examine these schedules, you will see that each has 4 R trials, and 8 N trials. The ratio (or density) of reinforcement is thus 4/(4+8) = 4/12 = 1/3. Or in other words, one out of three responses, on average, works. (Note that on the next 12 trials, the FR schedule should look exactly like the one above, but the VR schedule will be different, since it follows no fixed pattern, but is assigned randomly, so long as the right density is maintained.)

        As was the case with FR schedules, VR schedules with higher ratios (lower density of reinforcement) will show greater resistance to extinction. And if we compare VR and FR ratios to one another (where the ratio stays the same), then we will generally find that a VR schedule gives greater resistance to extinction than its corresponding FR schedule (though this is more likely at high ratios).

        Although it is a perhaps macabre example, Russian Roulette qualifies as a variable ratio schedule. So do lotteries and slot machines.

        In a fixed interval schedule (abbreviated FI), we establish a certain interval of time after which the first response works in obtaining the reward. In particular, responses during the interval are basically ignored by the experimenter: They are completely ineffective. Thus, in a FI2 schedule (where we will assume that the intervals are measured in minutes), the first response after a 2-minute interval works, whether that response comes immediately after the interval, or 5 hours later. An example of a fixed interval may involve the times at which you feed your pets. If you always feed them at the same times, then any response they make of going to the food area before the right time is ineffectual. Similarly, many people get paychecks on Friday afternoon, after they have put in a week's worth of work; going to get your paycheck before the proper time will not be an effective response.

        When does the next interval start? In the feed-your-pets example, the interval in some sense depends on how much time has passed. But normally, the intervals in these schedules are started after a reinforced response. Thus, on that account, an animal who doesn't respond until 5 hours after the end of the first interval gets the reinforcement at that time, and simultaneously causes the next interval to start counting down. These types of schedules are useful ways of probing an ability to judge the passage of time.

        As was the case with high ratios, long intervals lead to better resistance to extinction. So, an FI200 would be a better schedule to use than an FI3 if you want the learning to last while at the same time you want not to rely too heavily on always providing reinforcers. Again, you ought to be able to figure out why the Discrimination Hypothesis would also make this particular prediction. And as was true of the ratio schedules, high or long interval schedules are often taught through a process of weaning the animal to longer and longer waits.

        Our final simple schedule is the variable interval schedule (abbreviated VI). Much as was the case for the variable ratio schedule, the variable interval schedule involves presenting the animal with a series of intervals in an unpredictable order. Within any such series, of course, we can determine what the average interval might be. So, in an FI23 schedule, the interval will always be 23 minutes, whereas in a VI23 schedule, the average of the many different intervals will turn out to be 23. And as was the case when we compared fixed and variable ratios, a comparison of fixed and variable intervals will reveal that resistance to extinction will be stronger in the VI schedules, all other things (such as the average size of the interval) being equal.

        As an example of a VI schedule, imagine planning to buy something (a specific TV) at a store which is having a closing sale. The sale will start at 5 to 10% off, and over the next several weeks, will go to really spectacular savings such as 80% off. The problem you face is knowing when to buy, since more and more merchandise will disappear as the sale goes on. So, you can't wait a certain interval; instead, you will have to constantly check on how much of what you want is left as the prices get slashed, to try to get your best deal. That means you will respond a lot. And that is basically what happens in this type of schedule: a very high rate of response coupled with high resistance to extinction.

        Although these different types of schedules do have different effects on performance, comparing ratio to interval schedules can be a bit difficult. Nevertheless, we can look at such things as response rate with these. Let us restrict ourselves to variable schedules for the moment. With high ratios/intervals, one interesting finding that occurs is that responses tend to come faster in a variable ratio schedule than in a variable interval schedule. In a VR schedule using pecking as a response in pigeons, it is not impossible to find rates of over several hundred responses per minute! Such high rates are not often found with VI schedules, however. Indeed, rates over 100 responses per minute would qualify as high in VI.

        Also, the response curves tend to exhibit certain characteristics that seem to be schedule-specific in the fixed schedules, so long as the ratios/intervals are high. Thus, in the fixed ratio schedule, a very commonly reported finding involves what is called a post-reinforcement pause: After a response that works, there is a period of inactivity, and then the animal starts emitting responses in a relatively high burst, and at a relatively constant rate of speed. There will necessarily be some little pause in all schedules while an animal consumes its reinforcement, of course; the post-RF pause we are talking about here is an unusually long pause that extends well past the time to eat or drink.

        Let us go back to the feed-your-pets example to see what happens in a fixed interval schedule. In this example, you are not likely to have pets crowding underfoot as you move into the food area, if it is not their time to be fed. But, the closer to feeding time it is, the more likely it is that the animals will take an interest in your presence in the feeding areas. My cats, for example, are very likely to be underfoot (and a hazard to human locomotion!) when I go near their feeding areas within 20 or so minutes before the time I normally feed them. And that is basically also the pattern we find in the lab: Little or no activity immediately following a reinforcement, and then a gradual rise in activity as the interval winds down, with a very rapid burst of responses right towards the end. Because of the changing rate at which the animal responds, the impression one has in looking at the response rate following reinforcement is of a curve. That characteristic is referred to as a scallop. Figure 3 presents idealized response curves for the four schedules.

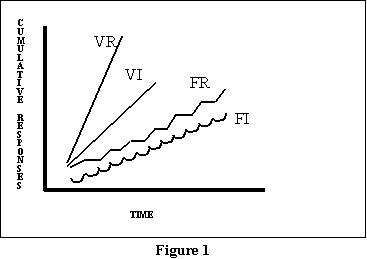        In this figure, as the lines slope higher and higher to the left, responding is getting faster and faster (since there will be more responses per some interval of time). That is why I have indicated a steeper line for VR (suggesting fastest responding in that situation). But do note the difference between the post-RF pauses in the FR schedule (the spots where the line goes flat), and the scallops in the FI schedule. Close inspection of real data collected using VR schedules will also occasionally show post-RF pauses, but these are of much smaller magnitude, and so easily missed. Normally, if you see a schedule with noticeable pauses or staircasing, it is a good bet that you have an FR schedule.
 
 
 

Other Schedules

        Three other types of schedule that may be briefly mentioned include chained, multiple, and concurrent schedules. In chained schedules, two (or more) schedules run in sequence, so that the animal has to perform according to the rules of both before being able to make a reinforced response. As an example, an FR10-FI2 schedule would require the animal to make 10 responses, following which a 2-minute interval starts. The tenth response meets the rule for the FR schedule, but instead of providing a reinforcer, it activates the second schedule (the FI schedule). So, it will be the first response that occurs after this interval is up that gets the reinforcer. If the animal only makes 9 responses, waits an hour, and then makes a tenth response, that doesn't get any reinforcement because the interval did not yet start. Conversely, in an FI2-FR10 schedule, a response made after the 2-minute interval is up would initiate an FR10 schedule, so that another 10 responses would be required before a reinforcer could occur. As you may imagine, chained schedules allow us to test the sensitivity of the animal to complex patterns.

        You have already read about one study using multiple schedules (and you will read about more below). In these, the animal has several training sessions, each of which may involve a different schedule. Thus, the experiment discussed above by Dyal and Sytsma provided two groups who differed in whether they had continuous reinforcement followed by partial reinforcement, or partial reinforcement followed by continuous reinforcement. Multiple schedules may be used to test sensitivity to changes in the animal's world, for example. We can set up several sessions such that the world is becoming an increasingly predictable place, or an increasingly unpredictable one (see the study by Hulse at the end of this chapter).

        And you have also read a bit about concurrent schedules. In these, the animal may typically choose any of several responses to make on a given trial (pressing the blue lever or pressing the red lever, for example), but each response will be associated with a different schedule of reinforcement! Herrnstein's Matching Law, described in Chapter 4, involved concurrent VI schedules. To remind you of what he found, animals tended to distribute their responses in proportion to the 'goodness' (measured by amount, density, or delay of reinforcement) of each: The response that led to the best outcome was made most often; the one that led to the second-best outcome occurred second-most often, and so on.

DRL & DRH Schedules

        A final set of schedules we will discuss include DRL and DRH schedules (standing, respectively, for differential reinforcement of low rates of responding, and differential reinforcement of high rates of responding). DRH schedules involve reinforcing the animal for making rapid responses. As you might imagine, such schedules are somewhat compatible with what an animal would do anyway, since rapid responses normally result in obtaining reinforcement sooner. Moreover, such rapid responding over a relatively long period of time should lead to getting more reinforcements. (Think of an animal on an FR30 schedule, for example, and allow it an hour in a Skinner box. An animal making its 30 responses at a relatively slow rate of speed will accumulate less rewards than an animal making its 30 responses at a relatively high rate.) Still, we can ask an animal to respond at a rate normally higher than it would, left on its own, and in such a case, we have a DRH schedule.

        Much more interesting are the DRL schedules (see, for example, the review article by Kramer and Rilling). In these, we reinforce the animal for waiting a certain amount of time between its responses. Specifically, an animal that responds too soon not only fails to get a reinforcer, but also resets the interval so that it now has to wait even longer between reinforcements. (If the interval we set is 20 sec, for example, an animal responding at 18 sec after the last reinforcer will reset the interval so that it must wait an additional 20 sec before responding: a total of 38 sec since the last reinforcer).

        Such schedules should remind you of the work we discussed earlier on omission training. As was true of omission training, DRL schedules are initially more difficult to acquire. They also tap into an animal's sensitivity to time. And as the interval in the schedule increases, the schedule becomes harder and harder to acquire. In DRL, the animal will typically make a number of non-reinforced responses (which is why this particular schedule qualifies as a partial reinforcement schedule, in case you were wondering!). Thus, in part because of these and because of the conditioning of waiting, a partial reinforcement effect is predictable.

        One more feature of DRL is of interest: Many of the animals during the waiting period do not wait passively. Instead, they engage in other types of stereotyped behaviors. This might remind you a bit of Skinner's discussion of superstitious behavior presented in Chapter 4, but it is really not the same thing: These responses occur well before the reinforcement (i.e., weak temporal contiguity, at best), which in any case is due to the final response that is not superstitious. Several theorists have speculated that these behaviors are ways in which an animal can time an interval. In this sense, they correspond a bit to our talking to ourselves ("one-thousand-one, one-thousand-two") as a way of estimating passage of time.

        With this as background, let us go on to consider the two most cited theories of the PREE. As we do, you may wish to consider how each might predict the findings with these various schedules.
 

C. Two Theories Of Partial Reinforcement

Amsel's Frustration Hypothesis

        The basic insight behind Amsel's theory is that an expectancy of reinforcement can cause frustration when it is not fulfilled. Failure to obtain an expected reward is an unpleasant experience. Amsel focuses on the consequences of frustration in accounting for partial reinforcement effects.

        One of the major concepts in the theory is that of the primary frustration response, R_F. The primary frustration response is the response that occurs on failure of reinforcement. Just as was true of the primary goal response we talked about in an earlier chapter (Chapter 4), the primary frustration response can be thought of as including a number of components, or fractions. These are presented in analogous fashion to the fractional goal responses; that is, they are conceived of as r_f...s_f units in which frustration has both the qualities of a response to a situation, and concomitant internal stimulation. As you might guess from the description so far, these r_f...s_f components can become mediators that become conditioned to various stimuli and responses in a situation. Thus, when an animal becomes frustrated in the presence of some stimulus S (or while doing some response R), various frustration mediators (biting, for example; or more generally, the tense feelings associated with frustration) may become associated with the S and the R. One thing about these that is critical for you to notice is this: There will be few or no such r_f...s_f mediators during acquisition for animals that are continuously reinforced, as they do not experience frustration. In contrast, animals that undergo partial reinforcement will have many of these r_f...s_f mediators present in their environments during learning.

        With this as background, we can now include three effects will characterize frustration, and that will depend on the presence of these mediators. In homage to the theories of extinction we looked at in an earlier section, these three effects are drive, discriminability, and response competition. Specifically, according to Amsel, frustration is an unpleasant drive that can motivate animals to avoid what has been frustrating them (due to the negative reinforcement of a decrease in frustration). At the same time, because it is a drive, it increases the overall activity level of the animal, which can eventuate in new responses, and thus, the possibility of learning competing responses to those that led to the frustration. And finally, the similarity of frustration experiences during learning and extinction can determine how much generalization there is between these two situations. Thus, the more different the frustration cues are in the two situations, the easier it will be to learn a new response during extinction (similar to what Mowrer and Jones claimed). Accordingly, Amsel's theory borrows a little bit from all the previous theories we've looked at, and by doing so, avoids problems that any single theory might have had.

        Let's first briefly look at evidence relevant to the drive and competing response effects of frustration, and then we'll talk about how the model plays its predictions out in continuous and partial reinforcement.

        In one famous experiment, Daly experimentally frustrated one group of rats by not feeding them in a spot where they had normally been fed before (similar to the procedure used by Seward and Levy). She then allowed these rats to learn a response that would get them away from this spot. There was no other reinforcer for learning this response other than escape from frustration. Nevertheless, the animals did acquire the response. Her argument was thus that getting away from some place where you've been frustrated is rewarding. This constitutes a claim that reduction in frustration acts as a negative reinforcer. You can now see how some such mechanism as this can account for the Seward and Levy findings on latent extinction.

        Another claim associated with the concept of drive is that increasing drive level ought to increase the overall activity level. That claim was in part examined by Amsel and Roussel. They trained rats to run to a goal box using continuous reinforcement for the first 80 or so trials. Following that, they switched to reinforcing only half of the trials. Following a non-reinforced trial, they observed faster running, consistent with a claim that these animals were aroused and energized. In a variant of this procedure, a dual-goal box alleyway was used in which the rats ran to goal box 1, and then after a short stay, were allowed to go through a door into an alley leading to goal box 2. These animals were always reinforced at the second goal box, but received reinforcements only half of the time at the first goal box. If they were not fed at the first stage, then (as in the first experiment), they ran faster to the second stage.

        Finally, what about competing responses? Energized behavior ought to result in the possibility of other behaviors being expressed. One of the observations a number of people have made (including Mowrer and Jones) is that frustrated animals engage in a much higher level of aggressive behavior. So, you can see from this the possibility of learning some sort of response that competes with the original because it involves getting rid of the frustration.

        Now that we've looked at some of the properties of frustration, let's discuss its effects on continuously reinforced responding. Here, the important point to note is that frustration will not be present during learning. The first point at which real frustration arises is when the animal hits the extinction phase. Hence, a frustration drive arises at extinction that can cause competing responses, and that opens up the possibility for negative reinforcement when the animal stops doing whatever it is that leads to frustration. At the same time, the presence of frustration cues during extinction (the r_f...s_f mediators) makes extinction a very different world or stimulus complex than learning. So, for all of these reasons, extinction following continuous reinforcement ought to be relatively quick.

        But can we say anything further than this? Fortunately, we can. Basically, Amsel has predicted that the bigger the difference there is in frustration between learning and extinction, the faster extinction ought to occur. (Note that this prediction specifically applies to the continuous reinforcement situation!) This should make sense to you on all three components of the theory: (1) Bigger frustration means more negative reinforcement, resulting in stronger learning; (2) bigger frustration means higher levels of arousal, resulting in more alternative behaviors from which competing responses may be acquired; and (3) bigger frustration means a greater discriminability between learning and acquisition, which should result in faster learning of a new response to the extinction situation. As you know from our discussion of results like Roberts's, animals that receive large reinforcers during learning show faster extinction. Losing a large reinforcer, of course, is more frustrating than losing a small reinforcer, so this finding fits in with the predictions.

        But what of partially reinforced animals? The important point here is that frustration cues (the r_f...s_f mediators) are present during acquisition. Because these cues are present, and on a number of trials become followed by reinforcement, they become classically conditioned cues for reinforcement. That is, the reinforcer is the UCS, while the frustration (the r_f...s_f mediators) is the CS. So, the animal learns that feeling frustrated is a cue or predictor for being fed, since feeling frustrated in the past has been followed by food. Put simply, we not only train animals to tolerate frustration, we also train them to reinterpret its significance: Instead of being a negative event, frustration becomes a signal for a positive event (the reinforcer).

        And of course, the higher the frustration the animal is exposed to during learning, the more similar learning will be to extinction (in which there is a very high level of frustration, indeed!). Thus, the second part of the prediction Amsel makes (confirmed by Roberts) is that partially reinforced animals ought to show a reverse reinforcement-size effect: Animals trained with large reinforcers should show greater resistance to extinction. Indeed, we can make this prediction for two very different reasons. One involves the afore-mentioned issue of discriminability: With larger reinforcers, there is a higher level of frustration on non-reinforced acquisition trials, making these more like extinction. But the second is that large reinforcers also act as more intense UCSs that result in better conditioning of the CS (the r_f...s_f mediators).

        In terms of drive level, then, high frustration during learning is 'good' and results in greater generalization, and more vigorous responding during learning (which will persist into extinction). At the same time, since the responding eventually succeeds in obtaining a reinforcer in the acquisition phase, competing responses are not acquired; the additional energization caused by frustration gets channeled into the learned response. And finally, of course, there are obvious implications for discriminability. Indeed, you can see that high ratios or intervals in partial reinforcement schedules should result in more frustration than low ratios or intervals. And intuitively, you should see that high ratios or intervals involve less discriminability because extinction can be defined as a very long sequence of time without reinforcement (which is what happens in high ratio/interval) schedules. The theory thus has the merit of being able to explain a number of effects with a few well-argued principles. Its claims regarding the opposite effects of reinforcement size in partial and continuous reinforcement are regarded as among its strongest successes.

Capaldi's Sequential Hypothesis

        An alternative approach has been championed by Capaldi. In his work, the stress will be on memory of events (as it was in the Wagner model of classical conditioning). As in Amsel's theory, there will be conditioning of cues that predict a reinforcer; and as in Amsel, there will also be a question of how similar these cues are in the learning and extinction environments. But, there is no specific mention of frustration as a mechanism in Capaldi's theory, and indeed, he has published some experiments claiming to find evidence against that mechanism. Rather, the focus is on non-reinforced trials. His basic idea has to do with how salient these become in an animal's memory. The longer the period of non-reinforcement during learning, the more salient these are.

        Several people have done studies attempting to determine how many pairings of a response and a reinforcer it takes in order to develop an expectancy of reinforcement: an ability to anticipate that a reward will follow the execution of a response. One way in which to do so is to adopt Amsel's claim that failed expectancies lead to frustration, and that frustration energizes behavior. In studies such as these, the question is, how many pairings do we need before we see that a non-reinforced trial changes the animal's behavior? In one such study, Hug claimed that at least 8 or so pairings were required.

        If that number is correct, then there are several studies demonstrating a partial reinforcement effect before expectancies have developed! One such study is by Godbout, Ziff, and Capaldi. They took several groups of animals and provided them with very small numbers of response-reinforcer pairings. In fact, these varied between two and five pairings (well below the minimum number that Hug claimed was necessary for frustration). Of course, we can include non-reinforced trials among these for some of our groups in order to assess a partial reinforcement effect. In any case, following this very brief acquisition period, we start the animals on extinction. Compared to animals that received only continuous reinforcement, the animals with partial reinforcement extinguished more slowly. And the point here, of course, is that if these animals had not developed frustration, then there should have been no opportunity to condition r_f...s_f cues, and thus, no way in which extinction and learning would have differed (in terms of discriminability) for the partially reinforced and continuously reinforced groups.

        Another study by Capaldi and Waters is even more interesting and suggestive. In this study, rats ran down an alleyway for a reinforcer. Capaldi and Waters provided slightly different acquisition experiences for three groups of rats, before putting them all through extinction. Their design was basically the following:

            Group         Phase 1                                                              Phase 2

            1                 5 continuously reinforced (CRF) trials             extinction
            2                 10 continuously reinforced trials                      extinction
            3                 5 non-RF trials followed by 5 CRF                   extinction

        The question they asked was whether the groups would all extinguish at the same rate. Note that Hug's work might suggest fastest extinction for Group 2, because that group has perhaps enough trials to develop an expectancy, resulting in frustration during Phase 2. However, the frustration hypothesis would seem to predict that Groups 1 and 3 should extinguish at the same rate. Both have had 5 continuously reinforced trials, and if Hug's conclusions are correct, neither should have developed the frustration mechanism. But suppose Hug is wrong, and animals can build up an expectancy in fewer than 8 trials, though perhaps not one strong enough to manifest itself in overtly energized behavior. Even if Hug's conclusions are wrong, Groups 1 and 3 should still extinguish at the same rate, because Group 3 should effectively act like a continuously reinforced group! The reason is that Group 3 starts out with non-reinforcement. Since they have had no previous experience of reinforcement, non-reinforcement in the first 5 trials cannot cause any frustration! Their expectancy starts to form on Trials 6 through 10, and that involves the same number of pairings (and therefore the same learning of an expectancy) as Group 1. Thus, the predictions that Amsel's theory could make in this experiment seem quite clear.

        As you may have guessed, Group 3 showed a partial reinforcement effect. It can't have been due to frustration and the r_f...s_f mechanism. It must therefore have been due to something else. That something else is what Capaldi's theory seeks to address.

        So what is it that is important about Group 3, and that can result in a PREE? According to Capaldi, the answer is that Group 3 had a sequence of non-reinforced trials that was terminated by a reinforced trial. His theory is called the sequential hypothesis because it is the sequence of non-reinforced trials that will prove critical.

        The theory is memory-based, as indicated above. The idea here is fairly simple. What happens after a trial becomes part of the animal's memory (specifically, its short-term or working memory, as in Wagner's model). Those memory traces will still be present when the animal undergoes the next trial. If there is a reinforcer on the next trial, then the memory traces get conditioned to the reinforcer. In this case, the reinforcer acts as the UCS, and the memory traces constitute the CS. Thus, the memory traces, through classical conditioning, come to predict the reinforcer.

        In extinction, the memory traces will include whatever experiences are associated with not being reinforced. Hence, to the extent that similar traces were conditioned during acquisition, learning and extinction will be similar: The animal in extinction will experience cues that keep 'promising' a reinforcer, thus motivating its continued responding. With that as an overview, let's focus on the specifics.

        We will start with a simplifying assumption that the animal's memory cues include being reinforced on previous trials, or not being reinforced on previous trials. We will, moreover, assume that the animal has one or the other of these states, but not both (but see the next section below for some contrary evidence!). The longer the animal has been in a particular state, the more salient that state is. Thus, an animal that has not been fed on the previous ten trials has a relatively salient or strong memory of non-reinforcement compared to an animal that has not been fed on a previous three trials. And of course, whatever state of memory the animal is in ceases the moment the opposite event occurs. So, an animal that is in the reinforcement state enters the non-reinforcement state when it hits a non-reinforced trial, and conversely, an animal in the non-reinforcement state enters the reinforcement state with its first reinforced trial. A very simple way of thinking about this is that an animal's working memory acts like a two-state toggle switch: Reinforcement toggles its working memory into the reinforcement state, and non-reinforcement toggles its working memory into the non-reinforcement state (much as a light switch being pushed up or down toggles the light on or off).

    Let us call the memory of non-reinforcement an N-memory (abbreviated M_N), and the memory of reinforcement an R-memory (abbreviated M_R). We can now indicate the salience or intensity of this state by adding a number that indicates approximately how long the animal has experienced the state. Since this number will be a function of how many past trials of reinforcement or non-reinforcement the animal has had, we can use the number of identical trials as a rough indicator of salience. Accordingly, an animal that has just finished its third non-reinforced trial will be in the M_N3 state, whereas an animal that has just finished its tenth reinforced trial will be in the M_R10 state. (We do not have to assume that animals can do anything like counting; the numbers here do not imply that! Rather, the idea is that there is some qualitative sense of how long an animal has been in a state, perhaps due to the state getting stronger with each additional repetition of a given event. Even though counting is not an issue here, however, you may enjoy looking at an article by Capaldi and Miller that claims rats can count!)

        One more concept needs to be added, although we have been talking about it implicitly. It is the notion of an N-length. An N-length is the run or number of non-reinforced trials in a row. The N-length, of course, determines the salience of the N-memory: As the N-length increases, the M_N state strengthens. In the Capaldi and Waters experiment presented above, for example, the N-length for Group 3 was 5, so that on the 6^th trial, the animals should have been in the M_N5 state.

        Given this, the point that will be important is that when an N-length is followed by a reinforcer (causing the non-reinforcement state to toggle to reinforcement), there will be conditioning of the M_N that was in the animal's working memory. This is because the M_N serves as the CS that is present when the UCS (the reinforcer) occurs. Thus, in Capaldi's theory, increased resistance to extinction in partially reinforced animals arises in part because the animal learns that the M_N state predicts upcoming reinforcement. And of course, the more similar the M_N state during learning is to the M_N state the animal experiences in extinction, the longer the animal will respond.

        Let's work through an example, in order to see this better. We will take animals that are repeatedly exposed to the same pattern, and we will assume that they have had prior training with this pattern, so that we are looking at trials in the middle of their acquisition. Let us assume the following pattern of reinforced and non-reinforced trials (using R and N for reinforced and non-reinforced trials, respectively):

            Trial:     R         R         N         N         R         R         R         N         N         N         R

What ought to be in the animal's working memory on each of these trials may now be indicated as follows:

            Trial:     R         R         N         N         R         R         R         N         N         N         R
      Memory:     M_R1    M_R2   M_R3    M_N1     M_N2    M_R1    M_R2   M_R3    M_N1    M_N2     M_N3

        Here, the first M_R1 occurs because the trial prior to the first trial above was an R-trial (recall that this pattern is constantly recycling, so look to its end to see what came immediately before!). But now, let us also ask what types of classical conditioning of memories occur. In order for there to be classical conditioning on a given trial, there has to be a reinforcer (an R). Essentially, two types of memory states are being conditioned here. On some trials, the animal has reinforcement cues from the previous trial when a reinforcement occurs (resulting in conditioning of the M_R state), and on other trials, the animal has non-reinforcement cues (involving conditioning of the M_N state). Using plus signs to indicate trials on which such conditioning occurs, we now obtain the following diagram:

            Trial:         R         R         N         N         R         R         R         N         N         N         R
      Memory:        M_R1    M_R2    M_R3    M_N1    M_N2    M_R1    M_R2    M_R3     M_N1   M_N2    M_N3
M_R Learned:       ++        ++                                           ++        ++
M_N Learned:                                                       ++                                                                    ++

        As you can see from this example, in this particular sequence of trials, there are four occasions on which a memory of reinforcement is paired with a UCS, and two occasions on which a memory of non-reinforcement is paired with a UCS. The pairing of a UCS with a memory of being reinforced is not terribly noteworthy for our discussion of extinction, because reinforcement cues by definition will not be present in extinction. So, we need not discuss that particular type of association any further. But the pairing of a UCS with the memory of non-reinforcement is quite another matter: Those two trials are where we train our animal to tolerate non-reinforcement similar to what it will experience in extinction.

        There are a number of principles we can derive from this approach, but here are three. The first (the Principle of N-length) is that resistance to extinction ought to increase as the N-length increases. The reason is that longer N-lengths mean longer M_N, which are more similar to the excessively long M_N the animal will experience in extinction. And indeed, Gonzalez and Bitterman, for example, have obtained this result. But then, you knew about that anyway, since we already discussed the finding when we talked about how increasing ratios and intervals led to greater resistance to extinction. In an FR200 schedule, for example, the N-length will be 199, compared to a N-length of 9 in an FR10 schedule.

        The second principle (the Principle of Transitions) is that resistance to extinction ought to increase with the number of transitions from N to R. A transition is the trial on which the N-length stops because a reinforcement has occurred. On this definition, wherever there is a transition, there will be a conditioning trial (involving pairing of M_N with a UCS). Thus, number of transitions corresponds directly to the number of times a CS and a UCS have been paired.

        The third principle (the Principle of Variability) is that resistance to extinction ought to increase as a function of the number of different N-lengths encountered. This principle doesn't refer to how many N-lengths the animal experiences (Principle 2 does that!), but rather how many different types of lengths the animal experiences. In our example above, there were two types of N-lengths: a length of 2 (resulting in M_N2) and a length of 3 (resulting in M_N3). Because that was a recurring pattern, the animal only ever experiences two different types of N-lengths until it hits extinction. On the other hand, it will have many, many transitions, and not just the two that appeared above. If the sequence above were repeated 200 times during learning, for example, then the animal will have experienced 400 transitions (since there are two transitions per sequence), but still only two different types of N-lengths.

        The Principle of Variability may be thought of as a principle of predictability. The more different types of N-lengths the animal has been conditioned to, the less certain it can be that the N-length experienced during extinction is different from what happened during learning. As in Amsel's theory, animals repeatedly trained to the same N-length may develop an expectancy of about when the N-length should terminate. Such an expectancy could help them discriminate between learning and extinction. Varying the N-length prevents that. And you also already know the evidence supporting this principle: Variable reinforcement schedules do indeed lead to greater resistance to extinction than fixed schedules, all other things being equal.

        So, to go back to the Capaldi and Waters (and Godbout et al.) studies, a PREE with very few trials is possible so long as there is a transition. In Capaldi and Waters's Group 3, for example, there was indeed one transition involving conditioning of an N-state.

        These aren't the only principles that govern what should happen here. Just like Amsel, Capaldi can also account for the reinforcement size effect. Thus, on a transition, a larger reinforcer means a stronger UCS, which means stronger learning. And of course, during continuously reinforced learning, animals never become conditioned to N-lengths, accounting for why these will extinguish relatively rapidly. Similarly, reinstating learning cues during extinction ought to slow extinction, whereas changing such cues ought to speed it up. You already know several studies that support that particular claim. Finally, disrupting the animal's memory prior to a transition ought to influence the success of conditioning, because it ought to change the N-memory.

        As a final example of work compatible with Capaldi's theory, we will examine a finding by Capaldi, Hart, and Stanley. In involves what is called ITR (intertrial reinforcement). In ITR, animals are given a reinforcement between trials that has nothing to do with a response, or indeed, with being in the experimental apparatus. To see what might happen, let us set up a number of groups. We will, again, assume that all groups are somewhere in the middle of their learning, and are receiving the same sequence (presented below) over and over again. We will use I for the ITR. Here is the sequence:

            Group                         Repeating Acquisition Sequence

                1                             R                 N                 N                 N                 R
                2                             R                 N       I        N                 N                 R
                3                             R                 N                 N       I        N                 R
                4                             R                 N                 N                 N       I        R

        The question is, what will happen when all of these groups are put through extinction? To see, let's add in the N-states:

            Group                         Repeating Acquisition Sequence

                1                             R                 N                 N                 N                 R
                                               M_R1            M_R2            M_N1            M_N2            M_N3

                2                             R                 N        I         N                 N                 R
                                               M_R1            M_R2  M_N1   M_R1            M_N1            M_N2

                3                             R                 N                 N         I        N                 R
                                               M_R1            M_R2            M_N1   M_N2   M_R1           M_N1

                4                             R                 N                 N                 N         I        R
                                               M_R1            M_R2            M_N1            M_N2    M_N3   M_R1

        Notice what happens. The ITR In Groups 2 and 3 chops up the N-length, because it toggles the state in the animal's working memory. Also, in each group, the ITR is associated with an N-length, so there should be some conditioning of the N-length to it (since it is a UCS, by definition). But whatever conditioning occurs to the ITR is completely irrelevant to extinction. The reason is that the animal is no longer in its apparatus, so that it is learning that when it has an N-state and it is in the spot where it has received ITR, expect a reinforcer. But when it is back in the apparatus, the environmental cues associated with where it received an ITR have been toggled to the experimental context cues, so that that particular expectancy is no longer in operation. Thus, the additional transitions and N-length variability caused by ITR do not influence what happens in the learning (and therefore, extinction) context. So, we need look just at where a transition occurs in the learning environment. For Groups 1 through 3, that transition occurs on the last trial. And as you can see from the table above, the N-state that gets conditioned on the last trial becomes smaller and smaller. By the Principle of N-length, then, we would expect less and less resistance. Capaldi et al. do indeed find that ITR inserted into an N-length reduces the resistance to extinction, as our discussion of the example above would suggest.

        What about Group 4? Rather surprisingly, the analysis above suggests that Group 4 ought to act in some sense like a continuously reinforced group! The reason is that the placement of ITR in Group 4 has prevented the conditioning of any N-state within the experimental context. That, in turn, suggests that partial reinforcement schedules may sometimes give results identical to continuous reinforcement schedules (or at least, fail to yield the usual PREE). We will see below some further evidence questioning whether greater resistance to extinction is always found with partial reinforcement.

        Although Capaldi's theory does an excellent job of handling a number of findings, it too, like Amsel's theory, has its problems. One such problem occurs in a study conducted by Hill and Spear. They put their animals through extinction under a fairly unusual set-up; namely, they ran one extinction trial per day. Since the contents of working memory do not last the whole day, this means that the animals during extinction ought always to have experienced a minimal N-state (namely, M_N1). Under these circumstances, animals conditioned with higher ratios ought to have more discriminability with the extinction conditions, and not less (M_N200 is more different from M_N1 than M_N2 is, for example). Thus, animals with higher ratios ought to have faster extinction, in contrast to the usual partial reinforcement findings. This prediction of Capaldi's, however, proved false. (And note that this study poses problems for Amsel, as well!)

        A second series of studies that also seems incompatible with Capaldi was done by Pavlik and colleagues (e.g., Pavlik and Carlton). They used concurrent schedules, except that instead of the two stimuli being present simultaneously, only one was present on a given trial.  Each stimulus, of course, was trained with a different schedule.  One of the schedules involved continuous reinforcement, and the other involved partial reinforcement. Thus, unlike the vast majority of studies in which different groups of animals experiencing different schedules were compared, these studies involved the same animals experiencing both types of schedules. And when that happens, the response on the continuous reinforcement schedule takes longer to extinguish. That is a curious finding, and it is hard to know what to make of it. I suspect that its ultimate explanation may turn out to involve components of a contrast effect. But in any case, since there were no N-lengths or frustration conditioned to the stimulus on the continuously reinforced schedule, neither Capaldi's nor Amsel's theory would elegantly handle this finding.
 

III. Complex Pattern Sensitivity

            Group             Phase 1             Phase 2             Phase 3                   Phase 4

                1                 Continuous       Continuous        Continuous             Extinction
                2                 Random            Random            Random                  Extinction

                3                 Continuous       Systematic        Random                  Extinction
                4                 Random            Systematic        Continuous             Extinction
 
        Of course, predicting what should happen in the first two groups is easy: There should be a partial reinforcement effect. The interesting question is what to expect in the last two groups. There are a number of possibilities here, depending on which set of theories you wish to apply. Using the Mowrer and Jones Discrimination Theory, and based on the results of the study by Dyal and Sytsma, for example, we might predict that Group 3 will be equal to Group 2, and that Group 4 will be equal to Group 1. This prediction is based on claiming that only what the animal has learned in the last phase before extinction is relevant. So, Groups 2 and 3 should have the same relatively low discriminability between Phase 3 and extinction, whereas the other groups should have the same relatively high discriminability.

        Alternatively, both Amsel's and Capaldi's theories may be used to predict that Groups 3 and 4 should be equal to one another. Each has had the same experiences, only in different order. On this account, each should have had the same number of conditioning trials involving frustration cues (r_f...s_f) or N-states (M_N) predicting reinforcement. Moreover, since there have been more of these trials in Group 2 than in Groups 3 and 4 (Groups 3 and 4 have one phase in which there is no such conditioning due to continuous reinforcement!), we may also predict that resistance to extinction in Groups 3 and 4 will be more than Group 1's resistance, but less than Group 4's.

        Now that we have our predictions, we can look at the results to see which of these two approaches is better supported. And the answer turns out to be that neither one is correct! It is certainly true that Group 3 has a very high resistance to extinction, much as does Group 2. But the surprise is that Group 4 shows the most rapid extinction. Even though they had two phases involving partial reinforcement, they show less resistance than a continuously reinforced group.

        What is going on, here? In fact, Hulse's finding fits in quite well with a type of cognitive expectancy theory of extinction. But instead of the type of expectancy found, say, in Amsel's theory (in which the animal is sensitive to what ought to happen on a given trial), the expectancy here is a dynamic one involving sensitivity to change and its consequences. If you go back and look at Groups 1 and 2, you will see that their experiences never change. The picture is very different for Groups 3 and 4, however. Group 3's world is becoming less and less predictable over time, since it is moving from continuous (perfectly predictable) to random reinforcement. In terms of metalearning (learning about learning), Group 3 should thus be learning to rely less and less on trying to predict or expect reinforcement. But such metalearning is precisely the type of result that should yield very high resistance during extinction. In cognitive expectancy theory, of course, animals need to acquire a new expectancy about extinction. That acquisition is triggered by evidence that the old expectancies are no longer valid. But in Group 3, an animal that isn't relying on making predictions won't be sensitive to when a prediction fails to come true, making the acquisition of a new expectancy difficult. (This may remind you a bit of what we talked about with respect to learned irrelevance or learned indolence).

        In similar fashion, Group 4's world is getting more and more predictable, going from complete unpredictability to complete predictability. They ought to be learning that the outcome of each trial increasingly can be taken to predict the outcome of the next trial. Thus, when they hit extinction, assuming a strongly predictable world, a non-reinforcement trial for them ought now to signal that the next trial will be a non-reinforcement trial, as well. Thus, we would expect them to show strong sensitivity to the change that occurs in extinction, resulting in extraordinarily fast adaptation. Being able to predict changing, evolving patterns in the world is a much more adaptive and useful skill than simply developing an expectancy of what should happen on Trial x based on the average of what has happened on all previous trials. The world changes; and organisms that are sensitive to such changes will be better situated to survive.

        A follow-up study by Fountain and Hulse demonstrates the same mechanism. They had rats run an alleyway for reinforcers. In an initial learning phase, all animals were given sequences of four trials in which each trial involved a different amount of reinforcement. There were considerable breaks between these sequences. Then, in a test phase, the rats were given a sequence of five rather than four trials, but on the fifth trial, there was no reinforcement. Three groups had the following setup:

            Group         Acquisition Sequence                     Test Sequence

                1             14     7     3     1                                 14     7     3     1     0
                2             14     5     5     1                                 14     5     5     1     0
                3             14     3     7     1                                 14     3     7     1     0

        As you can see, the first group had a very simple pattern in which the amount of reinforcement decreased steadily on every trial. In contrast, the other two groups also had patterns that ended with the smallest reinforcement, but their patterns were not as simple. Fountain and Hulse argued that if the rats were capable of learning a rule specifying the pattern, then Group 1 should do best, since theirs was the simplest rule (things are always decreasing from first to last trial). Consistent with this claim, Group 1 on their test sequence slowed their running considerably on the fifth trial, but the other two groups did not.

        This study is based on a claim that rats are capable of learning rules for how things are organized. That isn't the only theory that has been proposed to account for serial pattern learning. Capaldi, Verry, and Davison, for example, have claimed that serial pattern learning represents association learning in which the previous trial acts as the stimulus cue for the next trial. But that explanation cannot handle Fountain and Hulse's results, because the animals in the test sequence had never been exposed to a 0-reinforcer trial, and so could not have learned that a trial in which there was one reinforcer was the stimulus cue for a trial in which there were no reinforcers.

        In another, earlier experiment by Hulse, rats were trained on a five-trial pattern that involved either a simple or a complex rule. You can derive the rules by consulting the design below:

            Group             Acquisition Sequence

                1                 14     7     3     1     0
                2                 14     1     3     7     0

        In this case, an association learning model might predict that the fourth trial and the number of reinforcements the rat obtains on that trial become a predictor for the fifth 0-reinforcement trial. But if that is the case, then both groups ought to learn at about the same rate. A rule-based model, on the other hand, would predict that the simpler rule is more likely to be learned, so that Group 1 should show enhanced performance. Consistent with that latter model, Hulse found that the rats in the first group slowed down their running on the fifth trial more than the rats in the second group. Both indeed learned that the last trial in the sequence provided no reinforcement (as evidenced by the change in their running speeds), but the learning was more successful in the first group. And lest you think the results might have been due to the relative similarity of reinforcement amounts in the fourth and fifth trials, be advised that follow-up studies by Hulse and Dorsky repeated this experiment, but with the complex and simple patterns having the same reinforcement amount on the fourth trial (1 pellet).

        In general, animals are sensitive to changes. As reinforcement systematically increases across a repeating sequence of trials, so do their responses. Contrarily, as reinforcement systematically decreases, responses such as running slow down.

        A number of people now study animal sensitivity to patterns and sequences, in order to determine the types of rules animals can acquire. Some of this involves very sophisticated patterning such as birds' sensitivity to rhythm and pitch patterns (e.g., Hulse, Cynix, and Humpal). A good place to start, if you are interested in this work, is the section on Sequence Memory in the Roitblat, Bever, and Terrace volume on Animal Cognition. The notion of rule-based learning strongly suggests that there may be more going on in extinction than is suggested by models such as Amsel's or Capaldi's that focus on the (classical) conditioning that occurs on an individual trial. They also suggest an involvement of long-term memory (typically referred to as reference memory in animals) in addition to working memory. The sequences animals learn in some serial pattern experiments seem to extend well beyond the limits of working memory. They would thus appear to require an ability to compare what is going on now with what has gone on in the past.

        A final point deserves mention before we close out this chapter. In the real world, not every action results in a successful outcome. So, a learning mechanism that allows persistence in the face of non-reinforcement makes a lot of sense (see also Flaherty). The partial reinforcement effect may thus be seen as the outcome of an adaptive process. At the same time, the ability to acquire rules that are sensitive to change is also extraordinarily useful and adaptive. What happens with partial reinforcement may well depend on whether the situation calls for associational or rule based learning. It is in part the difference between static and dynamic expectancies.
 
 
 

Adelman, H.M., & Maatsch, J.L. (1955). Resistance to extinction as a function of the type of response elicited by frustration. Journal of Experimental Psychology, 50, 61-65.

Amsel, A. (1958). The role of frustrative nonreward in noncontinuous reward situations. Psychological Bulletin, 55, 102-119.

Amsel, A. (1962). Frustrative nonreward in partial reinforcement and discrimination learning: Some recent history and a theoretical extension. Psychological Review, 69, 306-328.

Amsel, A. (1992). Frustration theory: An analysis of dispositional learning and memory. NY: Cambridge U. Press.

Amsel, A., & Roussel, J. (1952). Motivational properties of frustration: Effect on a running response of the addition of frustration to the motivational complex. Journal of Experimental Psychology, 43, 363-368.

Baum, M. (1970). Extinction of avoidance responding through response prevention (flooding). Psychological Bulletin, 74, 276-284.

Boe, E.E., & Church, R.M. (1967). Permanent effects of punishment during extinction. Journal of Comparative and Physiological Psychology, 63, 486-492.

Capaldi, E.J. (1967). A sequential hypothesis of instrumental learning. In K.W. Spence & J.T. Spence (Eds.), The psychology of learning and motivation, Volume 1 (67-156). NY: Academic.

Capaldi, E.J. (1971). Memory and learning: A sequential viewpoint. In W.K. Honig & P.H.R. James (Eds.), Animal memory (111-154). NY: Academic.

Capaldi, E.J., Hart, D., & Stanley, L.R. (1963). Effect of intertrial reinforcement on the aftereffects of nonreinforcement and resistance to extinction. Journal of Experimental Psychology, 65, 70-74.

Capaldi, E.J., Lanier, A.T., & Godbout, A.C. (1968). Reward schedule effects following severely limited acquisition training. Journal of Experimental Psychology, 78, 521-524.

Capaldi, E.J., & Miller, D.J. (1988). Counting in rats: Its functional significance and the independent cognitive processes which comprise it. Journal of Experimental Psychology: Animal Behavior Processes, 14, 3-17.

Capaldi, E.J., Verry, D.R., & Davison, T.L. (1980). Memory, serial anticipation learning and transfer in rats. Animal Learning & Behavior, 8, 575-585.

Capaldi, E.J., & Waters, R.W. (1970). Conditioning and nonconditioning interpretations of small-trial phenomena. Journal of Experimental Psychology, 84, 518-522.

Daly, H.B. (1970). Combined effects of fear and frustration on acquisition of a hurdle-jump response. Journal of Experimental Psychology, 83, 89-93.

Dragoi, V., & Staddon, J.E.R. (1999). The dynamics of operant conditioning. Psychological Review, 106, 20-61.

Dyal, J.A., & Sytsma, D. (1976). Relative persistence as a function of order of reinforcement schedules. Journal of Experimental Psychology: Animal Behavior Processes, 2, 370-375.

Ferster, C.B., & Skinner, B.F. (1957). Schedules of reinforcement. NY: Appleton-Century-Crofts.

Flaherty, C.F. (1985). Animal learning and cognition. NY: Knopf.

Fowler, H., & Miller, N.E. (1963). Facilitation and inhibition of runway performance by hind- and forepaw shock of various intensities. Journal of Comparative and Physiological Psychology, 56, 801-806.

Fountain, S.B., & Husle, S.H. (1981). Extrapolation of serial stimulus patterns by rats. Animal Learning & Behavior, 9, 381-384.

Godbout, A.C., Ziff, D.R., & Capaldi, E.J.

Gonzalez, R.C., & Bitterman, M.E. (1964). Resistance to extinction in the rat as a function of the percentage and distribution of reinforcement. Journal of Comparative and Physiological Psychology, 58, 258-263.

Guthrie, E.R. (1952 ). The psychology of learning. (Revised edition) NY: Harper & Row.

Hammond, L.J. (1980). The effect of contingency upon the appetitive conditioning of free operant behavior. Journal of the Experimental Analysis of Behavior, 34, 297-304.

Herrnstein, R.J. (1970). On the law of effect. Journal of the Experimental Analysis of Behavior, 13, 243-266.

Heyes, C.M., Jaldow, D., & Dawson, G.R. (1993). Observational extinction: Observation of nonreinforced responding reduces resistance to extinction in rats. Animal Learning & Behavior, 21, 221-225.

Hill, W.F., & Spear, N.E. (1962). Resistance to extinction as a joint function of reward magnitude and the spacing of extinction trials. Journal of Experimental Psychology, 64, 636-639.

Hug, J.J. (1970). Number of food pellets and the development of the frustration effect. Psychonomic Science, 21, 59-60.

Hull, C.L. (1943). Principles of behavior. NY: Appleton-Century-Crofts.

Hull, C.L. (1952). A behavior system. New Haven: Yale.

Hulse, S.H.

Hulse, S.H. (1978). Cognitive structure and serial pattern learning by animals. In S.H. Hulse, H. Fowler, & W.K. Honig (Eds.), Cognitive processes in animal behavior (311-340). NJ: Erlbaum.

Hulse, S.H., & Campbell, C.E. (1975). "Thinking ahead" in rat discrimination learning. Animal Learning & Behavior, 3, 305-311.

Hulse, S.H., Cynix, J., & Humpal, J. (1984). Cognitive processing of pitch and rhythm structures by birds. In H.L. Roitblat, T.G. Bever, & H.S. Terrace (Eds.), Animal cognition (183-198). NJ: Erlbaum.

Hulse, S.H., & Dorsky, N.P. (1977). Structural complexity a a determinant of serial pattern learning. Learning and Motivation, 8, 488-506.

Hulse, S.H., & Dorsky, N.P. (1979). Serial pattern learning by rats: Transfer of a formally defined stimulus relationship and the significance of nonreinforcement. Animal Learning & Behavior, 7,211-220.

Kramer, T.J., & Rilling, M. (1970). Differential reinforcement of low rates: A selective critique. Psychological Review, 74, 225-254.

Lenderhendler, I., & Baum, M. (1970). Mechanical facilitation of the action of response prevention (flooding) in rats. Behavior Research and Therapy, 8, 43-48.

Light, J.S., & Gantt, W.H. (1936). Essential part of reflex arc for establishment of conditioned reflex. Formation of conditioned reflex after exclusion of motor peripheral end. Journal of Comparative Psychology, 21, 19-36.

Mackintosh, N.J. (1974). The psychology of animal learning. CA: Academic Press.

Maier

Mowrer, O.H., & Jones, H. (1945). Habit strength as a function of the pattern of reinforcement. Journal of Experimental Psychology, 35, 293-311.

Nevin, J.A. (1988). Behavioral momentum and the partial reinforcement effect. Psychological Bulletin, 103, 44-56.

Pavlik, W.B., & Carlton, P.L. (1965). A reverse partial-reinforcement effect. Journal of Experimental Psychology, 70, 417-423.

Pavlov, I. (1927). Conditioned reflexes. London: Oxford U. Press.

Rescorla, R.A. (1997). Response-inhibition in extinction. Quarterly Journal of Experimental Psychology. B. Comparative and Physiological Psychology, 50B, 238-252.

Roberts, W.A. (1969). Resistance to extinction following partial and consistent reinforcement with varying magnitudes of reward. Journal of Comparative and Physiological Psychology, 67, 395-400.

Roitblat, H.L., Bever, T.G. & Terrace, H.S. (Eds.), Animal cognition. NJ: Erlbaum.

Scavio, M.J. (1974). Classical-classical transfer: Effects of prior aversive conditioning upon appetitive conditioning in rabbits. Journal of Comparative and Physiological Psychology, 86, 107-115.

Seward, J.P., & Levy, N. (1949). Sign learning as a factor in extinction. Journal of Experimental Psychology, 39, 660-668.

Sheffield

Skinner, B.F. (1938). The behavior of organisms: An experimental analysis. NY: Appleton-Century-Crofts

Timberlake, W. (1980). A molar equilibrium theory of learned performance. In G.H. Bower (Ed.), The psychology of learning and motivation Vol. 14 (). NY: Academic.

Timberlake, W. , & Allison, J. (1974). Response deprivation: An empirical approach to instrumental performance. Psychological Review, 81, 146-164.

Tulving, E. (1983). Elements of episodic memory. Oxford: Oxford U. Press.

Wagner, A.R. (1976). Priming in STM: An information proessing mechanism for self-generated or retrieval-generated depression in performance. In T.J. Tighe & R.N. Leaton (Eds.), Habituation: Perspectives from child development, animal behavior, and neurophysiology. NJ: Erlbaum.

Wagner, A.R. (1978). Expectancies and priming in STM. In S.H. Hulse, H. Fowler, & W.K. Honig (Eds.), Cognitive processes in animal behavior (177-209). NJ: Erlbaum.

Wagner, A.R. (1981). S.O.P.: A model of automatic memory processing in animal behavior. In N.E. Spear & R.R. Miller (Eds.), Information processing in animals: Memory mechanisms. NJ: Erlbaum.

Wagner, A.R.,& Brandon, S.E. (1989). Evolution of a structured connectionist model of Pavlovian conditioning (AESOP). In S.B. Klein & R.R. Mowrer (Eds.), Contemporary learning theories: Pavlovian conditioning and the status of traditional learning theory (149-189). NJ: Erlbaum.

Welker, R.L., & McAuley, K. (1978). Reductions in resistance to extinction and spontaneous recovery as a function of changes in transportational and contextual stimuli. Animal Learning & Behavior, 6, 451-457.
 
 
 
 

1. Chapter © 1999 by Claude G. Cech