 Figure 3-1
Figure 3-1
Connectionism is a style of modeling based upon networks of interconnected
simple processing devices. This style of modeling goes by a number
of other names too. Connectionist models are also sometimes referred
to as 'Parallel Distributed Processing' (or PDP for short) models
or networks.1
Connectionist systems are also sometimes referred
to as 'neural networks' (abbreviated to NNs) or 'artificial neural
networks' (abbreviated to ANNs). Although there may be some rhetorical
appeal to this neural nomenclature, it is in fact misleading as
connectionist networks are commonly significantly dissimilar to
neurological systems. For this reason, I will avoid using this
terminology, other than in direct quotations. Instead, I will
follow the practice I have adopted above and use 'connectionist'
as my primary term for systems of this kind.
The basic components of a connectionist system are as follows;
I will describe each of these components in turn. Readers who
require further technical details should consult the general framework
for connectionist systems described by Rumelhart, Hinton and McClelland
(1987).
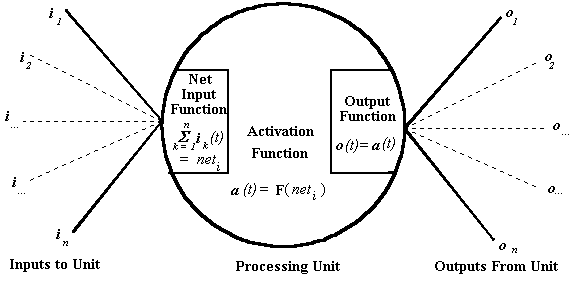
Processing Units
Processing units are the basic building blocks from which connectionist
systems are constructed. These units are responsible for performing
the processing which goes on within a connectionist network. The
precise details of the processing which goes on within a particular
unit depends upon the functional subcomponents of the unit. There
are three crucial subcomponents. These are,
The various components of a processing unit can be represented
as follows,
 Figure 3-1
Figure 3-1
The net input function of a processing unit determines
the total signal that a particular unit receives. The net input
function takes as input the signal which a unit receives from
all sources (ii-m), including the other units which
it is connected to. It is often the case that the net input function
of a unit is relatively simple. Commonly, the net input function
for a unit will just sum the of the input signals the unit receives
at a particular time (t).
The activation function of a particular unit determines
the internal activity of the unit, depending upon the net input
(as determined by the net input function) that the unit receives.
There are many different kinds of activation functions which particular
units can employ. The 'type' of a particular unit is determined
by its activation function. Perhaps the simplest kind of activation
function is illustrated below,
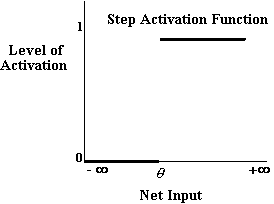
Activation functions such as this act rather like switches and are sometimes called 'step functions'. If the net input to a unit employing such an activation function is greater than some threshold value, q, the unit becomes fully active.3 If the net input is below this level, the processing unit is totally inactive. The activation function, aj, for such a unit, j, can be expressed more formally as follows;
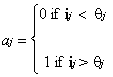
Activation functions of this kind were used in the very earliest
days of network research. Unfortunately though they are subject
to certain significant limitations (see Minsky & Papert 1968).
In particular, it is not possible to train networks which employ
this kind of unit arranged into more than two layers.
Currently, within the domain of trainable networks, by far the
most common kind of processing unit employed by connectionists
is what Ballard (1986) has called an 'integration device'. The
logistic function described by Rumelhart et al (1986a:
pp. 324-325), for example, is an instance of an integration device.
Integration devices have a sigmoidal activation function, similar
to the one illustrated below, and can be described as a continuous
approximation of a step function.
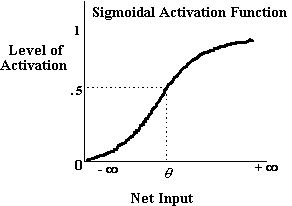
The activation function, aj, for a unit,
j, of this variety, receiving net input ij
is;
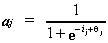
Integration devices include in their activation function something
known as 'bias'. Bias serves to alter the level of input to a
unit which is needed for that unit to become active and is therefore
analogous to the threshold of a step function. In more technical
terms, bias serves to translate the activation function along
an axis representing net input, thereby altering the location
of the activation function in net input space. The j
term in the logistic equation is the bias term of that activation
function.
One important feature of sigmoidal activation functions is that
they be differentiable. The reason this is important is that it
make it possible to train networks with more than two layers of
processing units, using powerful learning rules such as the generalized
delta rule, described by Rumelhart, Hinton and Williams (1986a:
pp. 322-328). This ability to train networks with multiple layers
has greatly increased the power of networks.
Although integration device units are arguably the most commonly
employed unit type in trainable networks at the current time,
other activation functions have also been explored. Recently,
Dawson and Schopflocher (1992) have described a kind of processing
unit which they call, following Ballard's (1986) terminology,
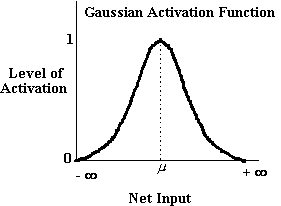
a 'value unit' . Value units employ a Gaussian activation function,
such as the one below,
The activation function, aj, for a unit,
j, of this variety, receiving net input ij
is;
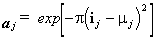
As the net input, ij, to a value unit
increases, the level of activation of the unit, aj,
increases, but only up to a certain point, j.
When ij = j, the activation
aj is maximized and has a value of 1.
If the unit receives net input greater than j,
the activation of the unit begins to decline again, down to 0.
As a consequence of having this kind of activation function, value
units will only generate strong activation for a narrow range
of net inputs. Value units, like integration devices, can be used
to construct trainable multilayered networks.
A unit in a connectionist network typically sends a signal to
other units in the network or to outside the network. The signal
that a unit sends out is determined by the output function.
The output function depends upon the state of activation of the
unit. It is common practice, at the current time, that the output
function of a particular unit is such that it just sends out a
signal equivalent to its activation value. However, there is no
theoretical reason why this must necessarily be the case.
Modifiable Connections
In order for a particular connectionist network to process information,
the units within the network need to be connected together. It
is via these connections that the units communicate with one another.
The connections within a network are usually 'weighted'. The weight
of a connection determines the amount of the signal input into
the connection which will be passed between units. Connection
weights (sometimes also called 'connection strengths') are positive
or negative real numerical values. The amount of input a particular
connection supplies to a unit to which it is connected is the
value of the result of the output function of the sending unit,
multiplied by the weight of the connection.
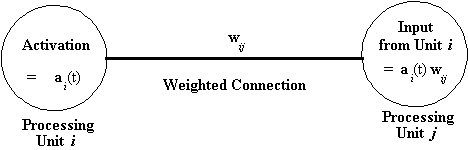
In principle, there is no limit to the number or pattern of connections
which a particular unit may have. Units can have weighted connections
with themselves and there can even be loops or cycles of connections.
However, for current purposes there is no need to explore such
complexities. Instead, attention will be limited to simple three
layered systems like the one illustrated below.
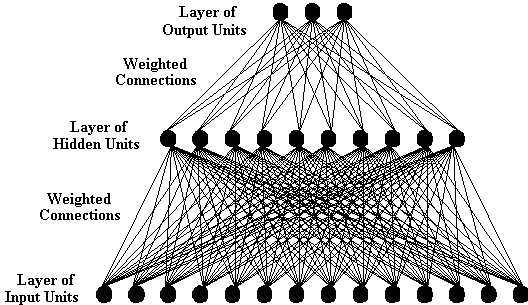
If particular processing units within a system can receive inputs
from sources external to the network itself, then these units
are usually called input units. Alternatively, if particular
processing units can send signals outside the network itself,
then these units are usually called output units. Finally,
processing units which can only directly communicate with other
units within the network (i.e. units which have no direct inputs
or outputs which are external to the network) are usually called
hidden units. Layers of hidden units are not an essential
feature of networks, although many networks require a single layer
of hidden units to solve a particular problems. It is also the
case that there is no reason why a network should just have a
single layer of hidden units. For example, a network described
by Bechtel and Abrahamsen (1991: p. 169) has two layers of hidden
units.
Learning Rules
A learning rule is an algorithm which can be used to make changes
to strengths of the weights of the connections between processing
units. Whereas all connectionist systems have processing units
and patterns of connections between the units, not all systems
have learning rules. Some networks (e.g. the Jets and Sharks Interactive
Activation and Competition network, described in McClelland and
Rumelhart (1988)) are built by hand (or 'hand-coded'). Hand-coded
networks have the weights of the connections between the processing
units set manually by the network's builder. However, in most
connectionist networks a learning rule of some kind is employed.
In this dissertation I will be concerned primarily with networks
that employ learning rules.
A learning rule is used to modify the connection weights of a
network so as (hopefully) to make the network better able to produce
the appropriate response for a given set of inputs. Networks which
use learning rules have to undergo training, in order for the
learning rule to have an opportunity to set the connection weights.
Training usually consists of the network being presented with
patterns which represent the input stimuli at their input layer.
It is common for connection weights to be set randomly prior to
training.
For example, consider one of the most popular learning rules for
connectionist networks, Rumelhart, Hinton and McClelland's (1986)
generalized delta rule. When using this rule, the network is shown
example patterns from a training set. The purpose of the generalized
delta rule is to modify the network's connection weights in such
a way that the network generates a desired response to each pattern
in the training set.
More specifically, with the generalized delta rule learning proceeds
by presenting one of the patterns from the training set to the
network's input layer. This causes a signal to be sent to the
hidden layer(s), which in turn results in a signal being sent
to the output layer. In the generalized delta rule, the actual
activation values of each output unit are compared to the activation
values that are desired for the input pattern. The error for each
output unit is the difference between its actual and desired activation.
The generalized delta rule uses this error term to modify the
weights of the connections that are directly attached to the output
units. Error is then sent through these modified weights as a
signal to the hidden units, which use this signal to compute their
own error. The error computed at this stage is then used to modify
the connection weights between the input units and the hidden
units. In every case, when a weight is changed, the generalized
delta rule guarantees that this change will reduce the network's
error to the current input pattern.
Usually, the learning rule only makes small changes to the connections
weights between the layers each time it is applied. As a result
training often requires numerous presentations of the set of input
patterns. By the repeated presentation of the training set and
application of the learning rule, networks can learn to produce
the correct responses to the set of inputs which make up the training
set. Learning rules thus offer a means of producing networks with
input/output mappings appropriate to particular tasks or problems.
Each presentation of the set of input patterns and output patterns
is known as an 'epoch' or a 'sweep'. When the network produces
an output for each input pattern which is close enough (as determined
by the experimenter) to the desired output for each pattern, training
stops and the network is said to have 'converged'.