SOME INFORMATION ON HIGH GRADIENT
MAGNETIC FIELDS
PONDEROMOTIVE MAGNETIC FORCES.
Each substance is magnetized in a magnetic field based on its magnetic
susceptibility ( ) which is substance-specific and
determines the
magnitude of the
magnetization I (magnetic momentum per unit
volume) by a superimposed magnetic field H,
such that I =
H in the Gauss system of units. The magnetic
susceptibility of a substance depends on its chemical composition, state, and density.
Substances with negative susceptibility are called diamagnetics and
) which is substance-specific and
determines the
magnitude of the
magnetization I (magnetic momentum per unit
volume) by a superimposed magnetic field H,
such that I =
H in the Gauss system of units. The magnetic
susceptibility of a substance depends on its chemical composition, state, and density.
Substances with negative susceptibility are called diamagnetics and  typically ranges
from -10-5 to -10-7 electromagnetic
units (emu). Substances with positive susceptibilities are referred to as
paramagnetics (10-3 10-7 emu). Common magnets are
ferromagnetic substances that are characterized by large values of
typically ranges
from -10-5 to -10-7 electromagnetic
units (emu). Substances with positive susceptibilities are referred to as
paramagnetics (10-3 10-7 emu). Common magnets are
ferromagnetic substances that are characterized by large values of  , 1 to 106 emu. Most biological substances are
diamagnetic, except for some proteins that contain metal ions, such as hemoglobin,
cytochrome, ferritin etc., which can be paramagnetic. However, some magnetobacteria
form ferromagnetic magnetite crystals.
, 1 to 106 emu. Most biological substances are
diamagnetic, except for some proteins that contain metal ions, such as hemoglobin,
cytochrome, ferritin etc., which can be paramagnetic. However, some magnetobacteria
form ferromagnetic magnetite crystals.
In a non-uniform field media with different magnetic susceptibilities are affected by
mechanical (poneromotive) forces including torque, magnetostriction, and a motive
force. For dia- and paramagnetic biological objects the magnetic susceptibility does not
vary with the superimposed field, and the net magnetic ponderomotive force acting on a
body of volume magnetic susceptibility  b
immersed in a medium of magnetic susceptibility
b
immersed in a medium of magnetic susceptibility  m in a magnetic field H is:
m in a magnetic field H is:
Eq.1
where V is the volume of the body, and (H2/2) the dynamic factor of
magnetic field, that describes its force action
In a gravity field the same particle is affected by two forces, gravity
Fgr and buoyancy
Fb. The correction for buoyancy yields
Eq.2 
where b, m are the densities of the particle and
medium respectively, and g is the gravity vector.
Comparing Eq.1 and Eq.2 we can calculate the dynamic factor of the field, in which
magnetic force acting on the body would be equal to gravity:
Eq. 3
The magnetic susceptibility and density of cytoplasm are about equal to that of
water. Since there are no data on the magnetic susceptibility of amyloplasts, we based
our original estimations on the value for starch. The magnetic susceptibility of water
w = -7.2×10-7 emu, and that of starch
st = -(8±0.2)×10-7, thus
the differential susceptibility = -8×10-8 emu. The density of
starch =1.5 g/cm3, and the density of
cytoplasm 1 g/cm3; therefore 0.5 g/cm3 and
/ = -6×106 (g/cm3)/emu. Therefore,
the dynamic factor (H2/2)
or HH necessary to exert a ponderomotive force comparable to gravity needs to be
about 3×109 Oe2/cm.
Generating a field above 2.4×104 Oe is technically difficult.
However, the dynamic factor (H2/2) can be
increased by reducing the dimensions of the area of non-uniformity of a magnetic field
and thus increasing the field gradient H. The precise calculation of the distribution of
field intensity, gradient, and dynamic factor for a particular magnetic system is difficult
but we can approximate the dynamic factor (H2/2) of the field as
((Hmax + Hmin)/2)*(Hmax -
Hmin)/d; where d is the distance over which the field
decreases from its maximal value Hmax to its minimal
Hmin. The achievable field strength Hmax from
permanent magnet systems is about 103 to
104 Oe, and in order to obtain the necessary gradient d needs to
be 10-2 to 1 cm which results in a high gradient magnetic field (HGMF).
There are several magnetic designs that can generate HGMFs with the required
parameters, the following text describes four that were used in our investigations.
MAGNETIC SYSTEMS
Small ferromagnetic particles form HGMFs with required parameters. For the
estimation of (H2/2) we can assume, that the magnetic field decreases
from its maximal value Hmax, on the surface of the particle to the
ambient filed over the distance d that is roughly equal to the diameter of the particle. If
the particle is small enough and magnetized to a high value (103 to
104 Oe) then HGMF with a significant dynamic factor (up to
1010 Oe2/cm) is present in its vicinity. If such a particle is
positioned close to e.g. a root cap, HGMF can displace amyloplasts inside the
columella cells providing a directional stimulus to the amyloplasts. One can distinguish
two possibilities:
The particle itself can be a permanent magnet. The induced field
B near an uniformly magnetized
(spherical) particle is described by the equation:
Eq. 4
where V- volume of the particle, I - its
magnetization, R - radius-vector
beginning at the particle center
(Fig. 1A). Around the particle the field gradient is directed towards the particle. If the
particle is not
spherical, the field distribution is more complicated, but the general pattern remains the
same.
Diamagnetics such as amyloplasts would be repelled from such a particle.
Alternatively, the particle can be a ferromagnetic substance that is magnetized by
an external field. The field in the vicinity of such a (spherical) particle is given by
Eq. 5
where Ho -
magnetizing field. The magnetic field near a magnetized particle consists of two zones,
in the "polar" areas the gradient is directed toward the particle, in the "equatorial area"
away from it (Fig. 1B). In the polar region amyloplasts would be pushed away from the
particle and in the equatorial zone attracted toward the particle and consequently
positively gravitropic roots should curve away from "polar areas" but toward the
"equatorial area", negative gravitropic shoots should show opposite curvature.
Assuming the same size and shape of the particle the field and the gradient can be
stronger for (B) but the distribution of the field, and the mutual positioning between
tested organ, the particle and external field is more complicated. For (A) special care
needs to be taken to prevent interaction of the particles with external magnetic fields
and each other. A substantial advantage of both magnetic systems is their small weight.
The main disadvantage are the small size of the HGMF area and difficult manipulations
of such small objects.
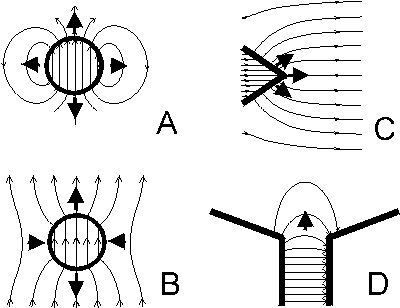
Figure 1. Magnetic systems used to generate high
gradient magnetic fields (HGMF). The density of field lines is proportional to the field
intensity, arrows indicate the direction of force acting on diamagnetic substances. The
field around a spherical permanent magnet diminishes with increasing distance,
resulting in a strong gradient when the sphere is small (A).
Diamagnetics would be repelled from the sphere. Magnetic field in the vicinity of a
ferromagnetic sphere magnetized by a (uniform) external magnetic field
(B). Diamagnetics would be repelled from the sphere in "polar"
regions and attracted to the sphere in "equatorial" area. The field in the vicinity of a
ferromagnetic wedge magnetized by a (uniform) external magnetic field
(C). A diamagnetic body would move away from the wedge
edge. HGMF at the edge of a gap between two magnets or magnetic poles will push
diamagnetics away from the gap (D).
The magnetic field near the tip of an externally magnetized ferromagnetic cone or
wedges stronger than the external magnetic field, so the gradient H is directed toward
the tip or edge of the ferromagnetic insert. Therefore a paramagnetic body would be
attracted to the tip, and diamagnetic particles such as amyloplasts are repelled from the
wedge (Fig. 1C). Therefore root curvature can be expected to occur away from the
wedge or cone and shoots are expected to curve toward the wedge edge. The dynamic
factor of HGMF around the wedge tip can be estimated as:
Eq. 6
where d is the dimension of the HGMF area,
I is the magnetization of the wedge. If the
ferromagnetic wedge is magnetized approximately to saturation
(Bsat =
Ho +
4Isat., 15 to 24
kGauss), and if d is 0.1 to 0.3
mm, then (H2/2) can be estimated to be 109 to
5×1010 Oe2 cm-1. The force acting on
amyloplasts within d is equivalent to or greater 1
g. The dynamic factor of the field
gradually decreased from this value by 1 to 2 orders of magnitude between 0.5 to 1.5
mm from the edge. The diameter of the plant rots and shoots
used in our experiments varied from 0.4 to 1.5 mm, such that amyloplasts at the
side opposite of the plant organ experienced a considerably reduced force, less than
10-1 g.
Therefore, the ponderomotive forces
acting on amyloplasts equal to gravity are confined to a small area of the plant tissue.
The system combines high values of the dynamic factor of the HGMF with a small size
of the area of non-uniformity. Since mutual positioning of seedling and wedge or cone is
relatively easy, such a magnetic system is suitable for the exploration of the spatial
distribution of sensitivity of statocytes to amyloplast displacement.
The edge of a gap between two magnets or magnetic poles is also suitable to
provide HGMFs with the necessary parameters. The field intensity decreases from the
depth of the gap towards the edge (Fig. 1D), therefore the gradient is directed toward
the depth of gap and perpendicular to the edge. Diamagnetic amyloplasts experience a
force directed away from the depth of the gap. Since the gap width represents the
extent of the HGMF d for the estimation of (H2/2), the field intensity and
gradient decrease as d increases. The force value in the gap area can vary from
negligible to about 1 g. Since the gap
width cannot be smaller than the experimental plant organ this system produces
relatively small gradients and the ponderomotive forces compare to the system
described above. However, the volume of HGMF can be larger and it does not require
precise mutual positioning of the magnetic system and plant tissue as the previously
described systems. Roots are expected to curve away from the depth of the gap near
its edge, shoots are expected to grow into the gap.
MAGNETOGRAVIPHORETIC MEASUREMENTS OF SMALL PARTICLES.
Initially, the estimations of magnetic susceptibility and density of amyloplasts were
assumed to be equal to that of starch but for the calculation of the forces that affect
amyloplasts in a HGMF of a particular magnetic system it is necessary to measure the
actual value of the ratio of differences in susceptibility and in density, i.e. the parameter
/. Values of magnetic susceptibilities and densities are necessary to estimate the
ponderomotive forces in a given system, to analyze the starch content of amyloplasts,
assess species differences and evaluate the contribution of the membrane envelope on
amyloplast motility.
The large heterogeneity of biological systems requires that such studies be
conducted on the cellular and subcellular level. Ideally one would study individual
amyloplasts. But the measurements of magnetic susceptibility of such small particles (1
to 5 µm in diameter) is difficult and traditional magnetometry methods (Faraday balance,
vibrating magnetometer, etc.) are not appropriate. Even superconducting quantum
interference devices (SQUIDs) are not sensitive enough to measure the magnetic
susceptibility of single amyloplasts. In contrast, particle magnetophoresis is suitable for
the determination of the magnetic susceptibility of single amyloplasts. Two
modifications of the method exist: Magnetic levitational suspension determines where
the particle comes into equilibrium and maintains a steady position within a known
(H2/2) and the magnetograviphoretic technique.
The later method is based on measurements of velocities of the movement of
particles that are suspended in liquid with a known density and magnetic susceptibility
inside a magnetic system that generates a HGMF with known parameters. Typically
particles that are more diamagnetic than the medium are measured with a
Brownback-type magnetic system that consists of a gap between magnetic poles with a
concavity on the top side. For paramagnetic particles a magnetic system with a
combination of a wedge-shaped and a concave magnetic pole is used. For biological
objects water or buffers are used as medium.
If a particle moves in the medium, it is subjected to the viscous friction force
Ffr. For the typical velocities the
movement of amyloplasts can be considered laminar (Reynold's number Re = Rv/
10-6 to 10-7 « 1), and
Ffr =
-v/, where is the mobility of the particle and
v the velocity. The velocity of the movement is
proportional to the net force (Fnet)
acting on the particles:
Eq. 7
Near the upper edge of the gap between the poles the field gradient H and dynamic
factor of the field (H2/2) are directed toward the gap (Fig. 2B). In the
absence of a magnetic field, the particles are sedimenting due to gravity
Fgr and buoyancy Fb and sediment when
Fb < Fgr (Fig. 2C):
Eq. 8
When the magnetic field is active, diamagnetic particles in this area experience an
additional, upward directed ponderomotive force
Fm (Fig. 2D). If
Fm >
Fg the particle moves upward with
the velocity:
Eq. 9
Due to the geometry of the field the movement of the particles in the area of
measurement is vertical and both equations can be written in scalar form:
Eq. 10
Eq. 11
Since all physical parameters that affect the mobility are identical for up- and
downward movement
neither size or shape of particles nor the viscosity of the solution need to be
determined. Measuring the
velocities of the particles in the absence
(vsed) and presence of HGMF
(vup), permits the calculation of
the
ratio of differential susceptibility and density /:
Eq. 12
The ratio (H2/2)/g is a calibration factor specific for the magnetic
system used to measure
(vup+vsed/vsed).
If density of the particles and medium, and magnetic susceptibility of the medium are
known, the
magnetic susceptibility of the particles can be determined.
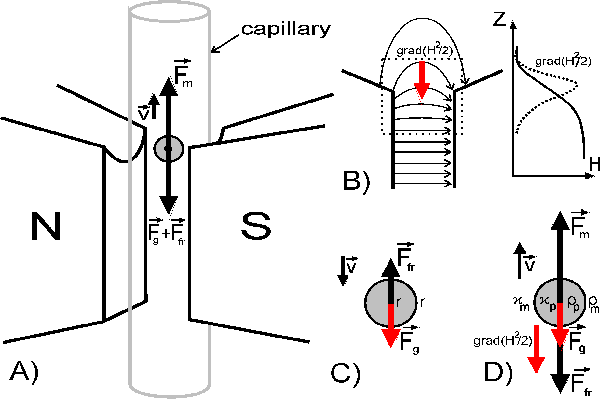
Figure 2. The principle of magnetograviphoretic
measurements of magnetic susceptibility of small particles. Sketch of the measurement
area of the device and forces that act on particles (A). The
distribution of magnetic field intensity and gradient in the gap between magnetic poles
(B), dotted square represents the area of measurements.
Forces acting on particle, immersed in liquid with different density and magnetic
susceptibility , sedimenting in gravity field (C) and moving
under the action of ponderomotive forces in non-uniform magnetic field
(D).
 ) which is substance-specific and
determines the
magnitude of the
magnetization I (magnetic momentum per unit
volume) by a superimposed magnetic field H,
such that I =
H in the Gauss system of units. The magnetic
susceptibility of a substance depends on its chemical composition, state, and density.
Substances with negative susceptibility are called diamagnetics and
) which is substance-specific and
determines the
magnitude of the
magnetization I (magnetic momentum per unit
volume) by a superimposed magnetic field H,
such that I =
H in the Gauss system of units. The magnetic
susceptibility of a substance depends on its chemical composition, state, and density.
Substances with negative susceptibility are called diamagnetics and  typically ranges
from -10-5 to -10-7 electromagnetic
units (emu). Substances with positive susceptibilities are referred to as
paramagnetics (10-3 10-7 emu). Common magnets are
ferromagnetic substances that are characterized by large values of
typically ranges
from -10-5 to -10-7 electromagnetic
units (emu). Substances with positive susceptibilities are referred to as
paramagnetics (10-3 10-7 emu). Common magnets are
ferromagnetic substances that are characterized by large values of  , 1 to 106 emu. Most biological substances are
diamagnetic, except for some proteins that contain metal ions, such as hemoglobin,
cytochrome, ferritin etc., which can be paramagnetic. However, some magnetobacteria
form ferromagnetic magnetite crystals.
, 1 to 106 emu. Most biological substances are
diamagnetic, except for some proteins that contain metal ions, such as hemoglobin,
cytochrome, ferritin etc., which can be paramagnetic. However, some magnetobacteria
form ferromagnetic magnetite crystals.












