Research

My research program lies within Mathematical Biology, Dynamical Systems and Mathematical Modeling. With collaborators and students, we appy differential equations and stochastic processes to model dynamics, evolution and genetics of biological populations. The process involves constructing mathematical models for conducting analysis using tools from dynamical systems, networks and numerical methods, along with biological theory and data, in order to gain insight on the fate of populations and structure of ecosystems. Below is more detail on current research topics.

Dynamics of eco-evolutionary networks and virus-immune interactions

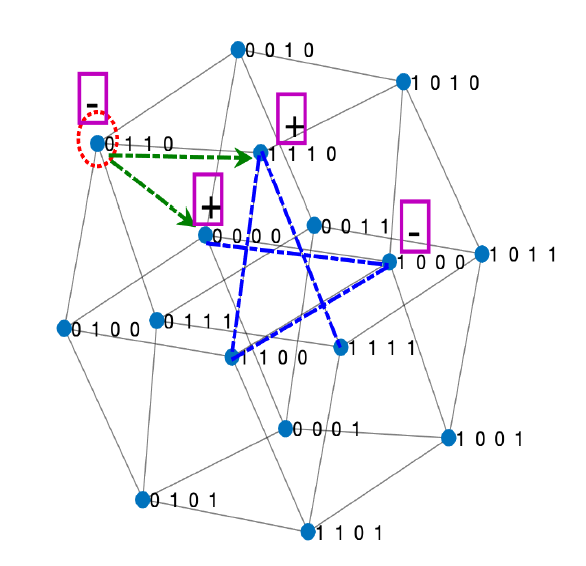
An emerging field in Mathematical Biology is eco-evolutionary dynamics seeking to unite ecology and evolution in population models. Our recent research establishes a novel network modeling framework with methods from dynamical systems, combinatorics, computation and stochastic processes to reveal patterns in evolution of ecosystems. We connect evolutionary genetics to population dynamics by constructing differential equation and stochastic ecosystem models with binary sequence representations of phenotypic traits mapping to fitness landscapes.

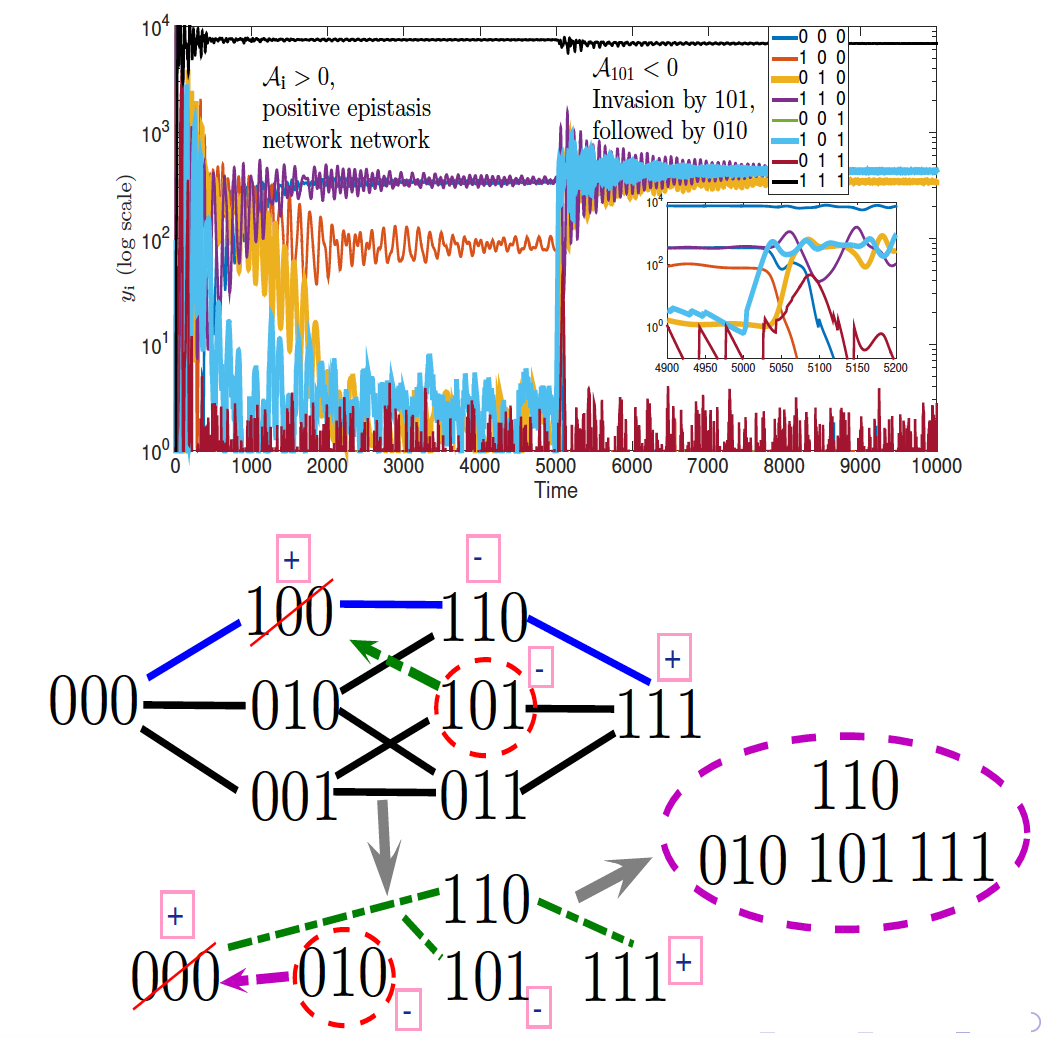
For example, in work on viral strain resistance to immune responses, we prove that bifurcations are determined and simplified by a certain measure of nonlinearity in the map from viral sequences to fitness landscape known as epistasis. The results can have implications for HIV immunotherapy and vaccine design, and generalize to decipher stability, structure and invasion of ecological networks based on an algebra of prey genetic sequences encoding predation and fitness trade-offs.

This work on virus and immune response network dynamics is currently supported by NSF grant DMS 1815095.

Selected Publications

• Browne, C.J., Yahia, F. Virus-immune dynamics determined by prey-predator interaction network and epistasis in viral fitness landscape . Journal of Mathematical Biology 86, 9 (2023).
• Browne, C. J., & Smith, H. L. (2018). Dynamics of virus and immune response in multi-epitope network. Journal of Mathematical Biology, 77(6), 1833-1870..
• Browne, C. (2016). Immune response in virus model structured by cell infection-age. Mathematical Biosciences & Engineering, 13(5), 887.
• Browne, C. J. (2015). A multi-strain virus model with infected cell age structure: Application to HIV. Nonlinear Analysis: Real World Applications, 22, 354-372.

Application of eco-evolutionary models to phylogenetic data

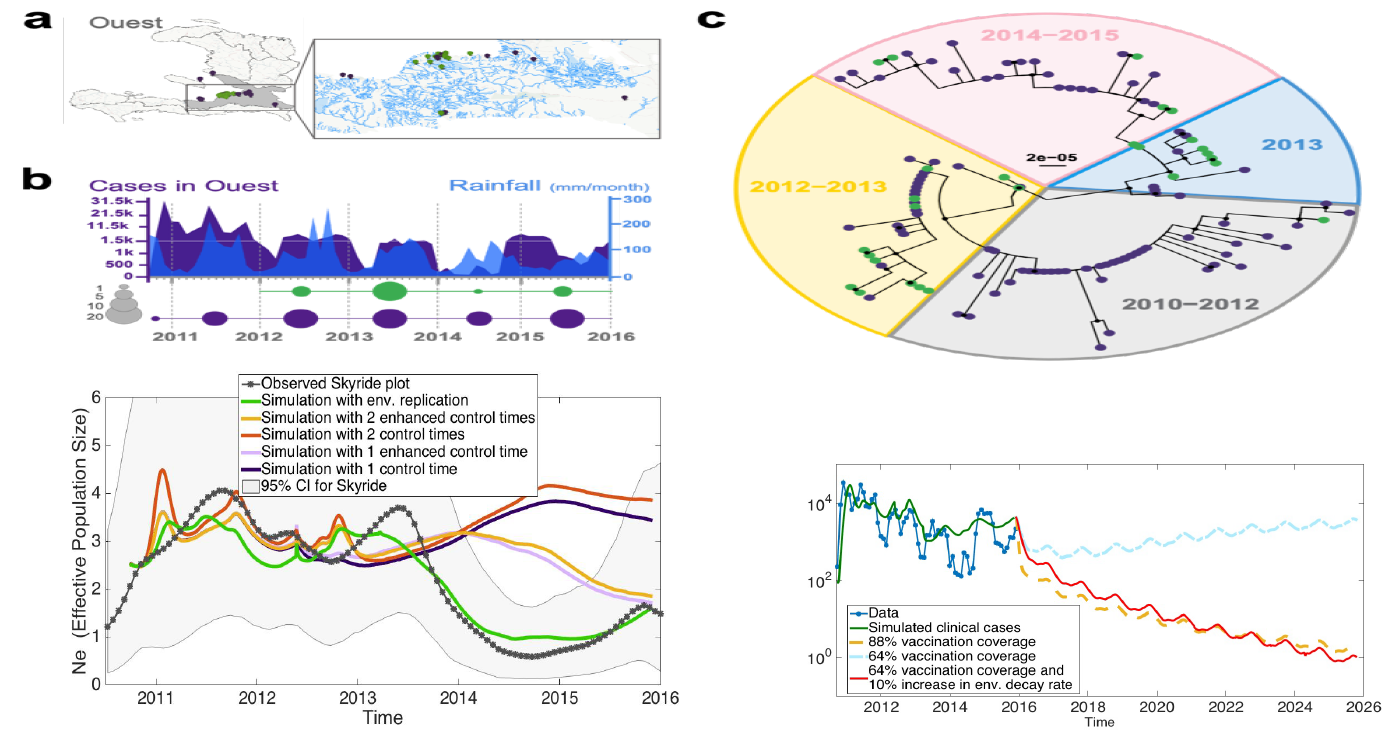
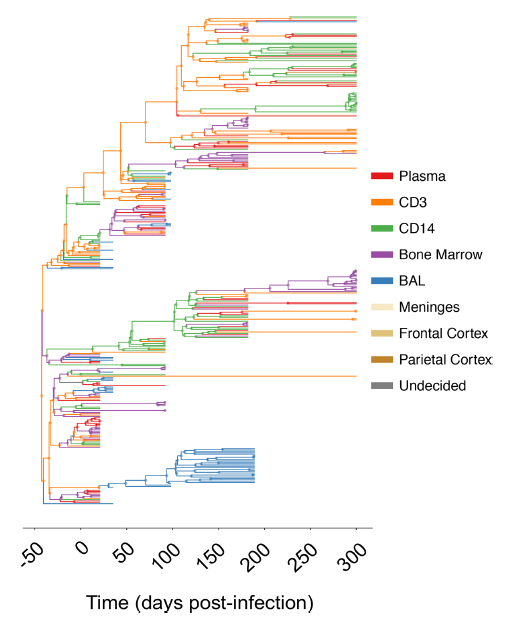
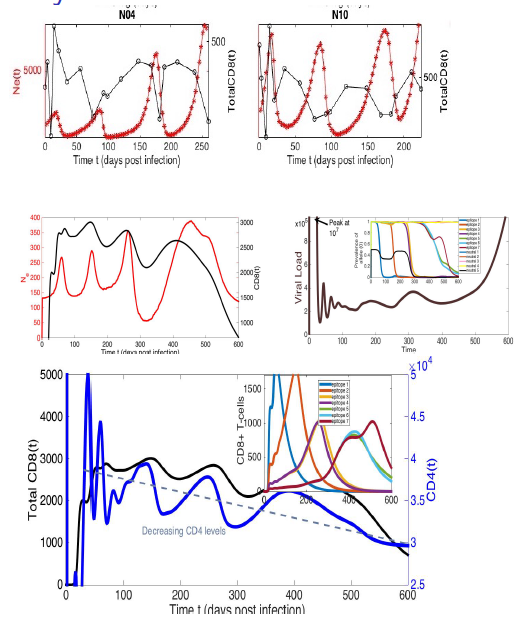The rise in genomics has amplified the need for connecting traditional population dynamics with evolutionary genetics. There is a need for computational tools to simulate eco-evolutionary dynamics, and validate with both genetic and population census data. In our recent work, we leverage genetic and census data, phylodynamic inference, and simulate eco-evolutionary dynamics to recapitulate the population genetic diversity measure of effective population size, shedding light on evolutionary forces in SIV-immune response experiments and the cholera outbreak in Haiti, along with assessing impact of "hidden transmission" during COVID-19 pandemic.

Selected Publications

• B. Rife Magalis, P. Autissier, K. Williams, X. Chen, C. Browne & M. Salemi, (2021). Predator-Prey Dynamics of Intra-Host Simian Immunodeficiency Virus Evolution Within the Untreated Host. Frontiers in Immunology , 4191.
• M. Giovanetti, E. Cella, F. Benedetti, [& 25 others, including C. Browne] (2021). SARS-CoV-2 shifting transmission dynamics and hidden reservoirs limited the efficacy of public health interventions in Italy. Communications Biology, 4(1), 1-9..
• C. Mavian, T. K. Paisie, M. T. Alam, C. Browne, V. M. Beau De Rochars, S. Nembrini, M. N. Cash, E. J. Nelson, T. Azarian, A. Ali, J. G. Morris Jr., M. Salemi (2020). Proceedings of the National Academy of Sciences, 117(14), 7897-7904.

Opitmization and resonance of periodic forcing in biological systems

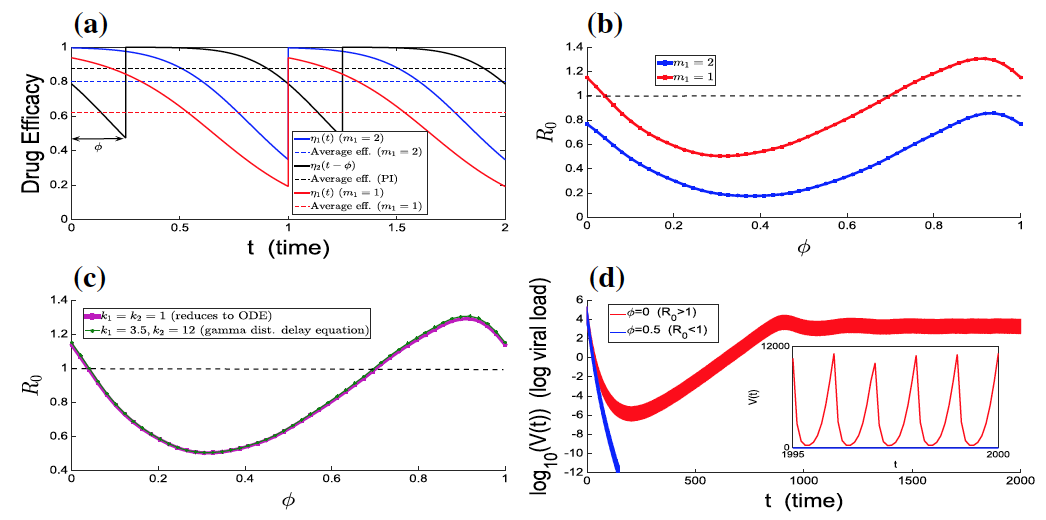
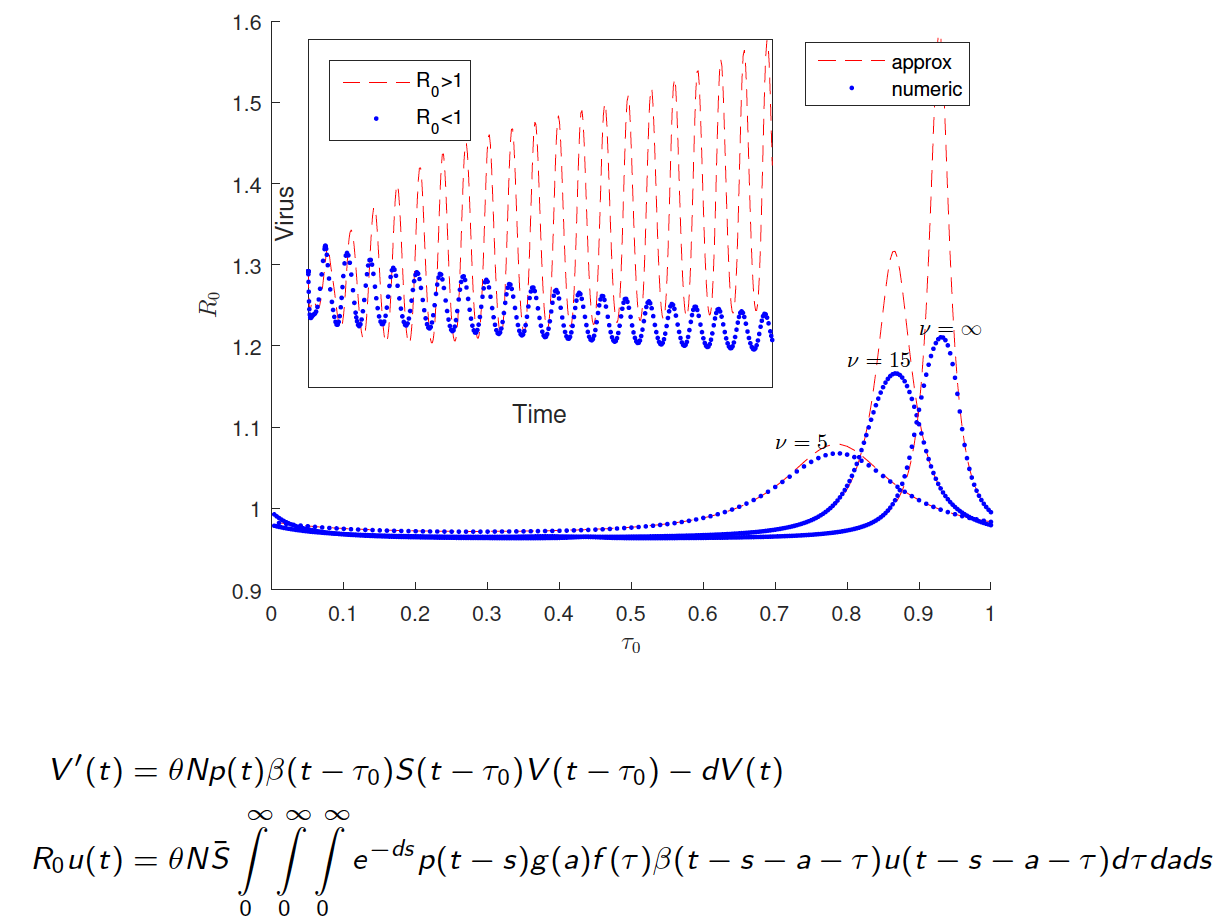
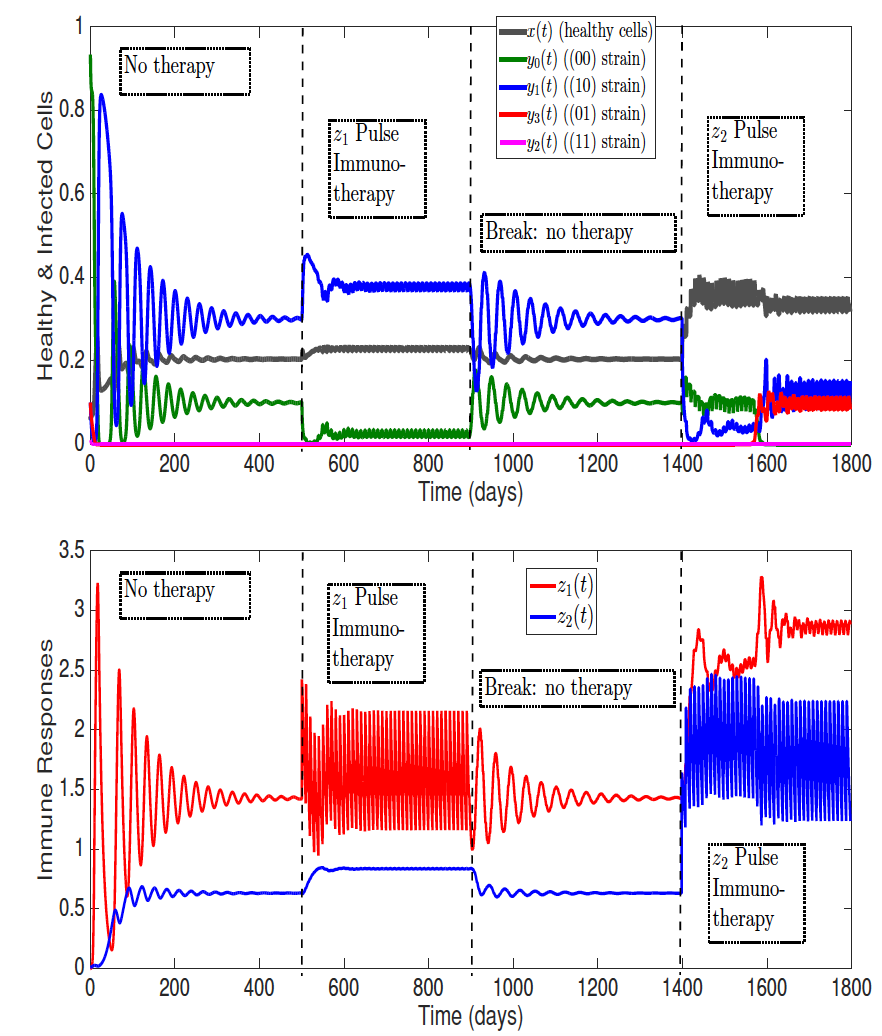Resonance between some natural period of an epidemic, infection or any biological system, life cycle or spatial structure and periodic parameters, along with the optimal timing of multiple periodic treatments or interventions, have been the subject of intensive study due to potential nonlinear impacts on population dynamics. In our work, we have advanced functional analysis and computation of periodic differential and infinite-dimensional integral equation systems to formulate reproduction number in periodic environments.

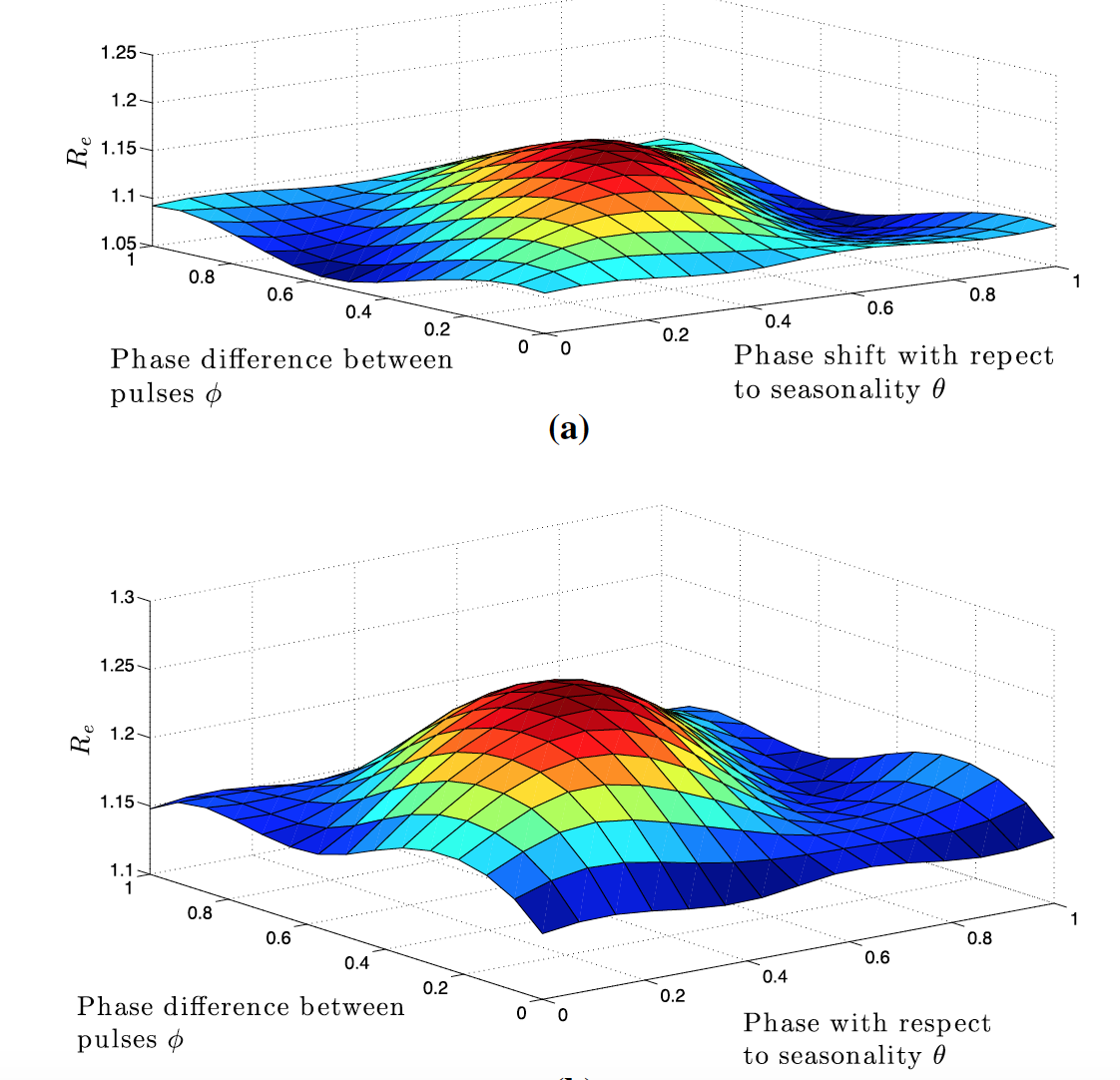We explore how the intracellular viral replication cycle interacts with combination antiviral drug kinetics and optimal deployment of mass (pulse) vaccinations across multiple connected regions against the seasonal water-human transmission of polio and cholera. Interestingly, we find that the relative timing of key replication parameters and distinct period control measures can differentially alter disease outcomes. Current and future work investigates optimal regimens of drug treatments or immunotherapies when drug or immune resistant strains evolve.

Selected Publications

• C. Browne, X. Pan, H. Shu, and X. S. Wang (2020). Resonance of Periodic Combination Antiviral Therapy and Intracellular Delays in Virus Model. Bulletin of Mathematical Biology, 82 (2), 29.
• C. Browne, L. Bourouiba, and R. Smith (2015). From regional pulse vaccination to global disease eradication: insights from a mathematical model of poliomyelitis. Journal of Mathematical Biology,71(1), 215-253.

Mathematical epidemiology

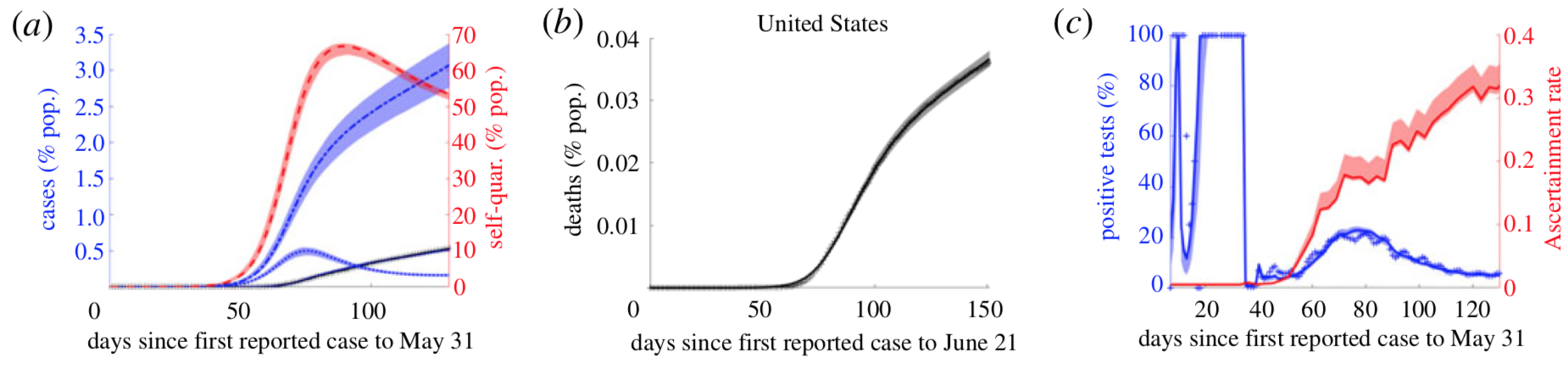
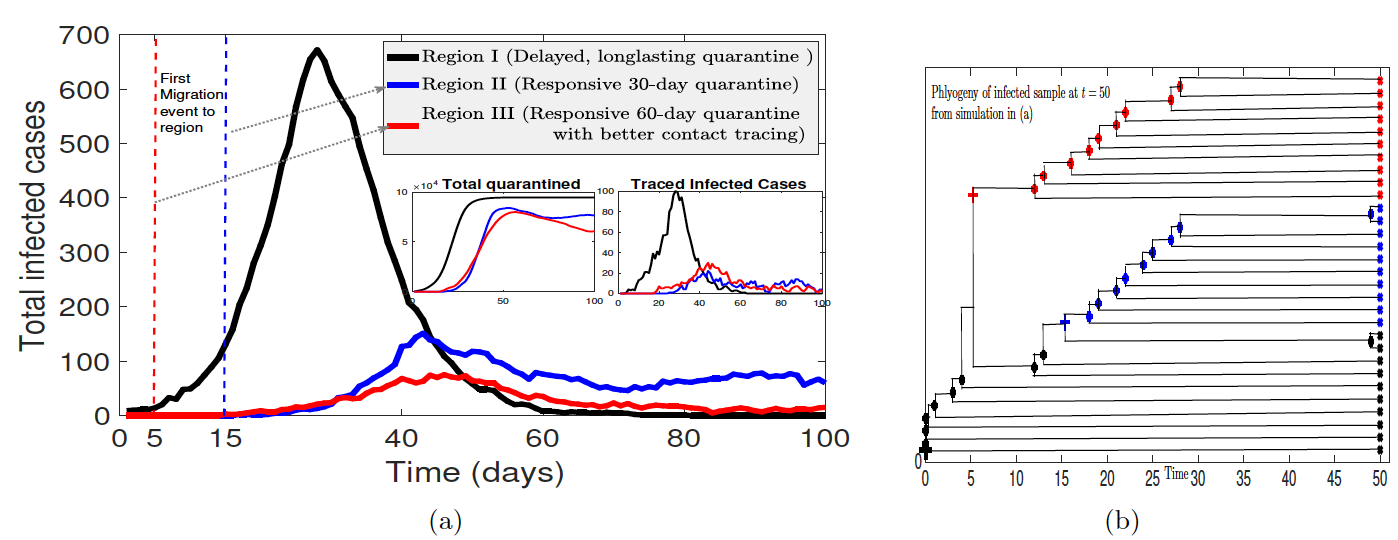
Traditionally the influence of control strategies on outbreaks has been investigated in compartmental ordinary differential equation models of the susceptible-infected-recovered (SIR) type with constant rate parameters. However both analytical and parameter estimation approaches are challenged by the dynamic nature of control strategies as public health authorities and individuals react to an evolving outbreak. By mathematical modeling contact-based interventions, such as contact tracing and lockdowns, as reactive quarantine measures, dependent on current infection rates, with different mechanisms of action, we analytically derive distinct nonlinear effects of these interventions on reproduction number, R_0, along with final and peak outbreak size. Furthermore, we simultaneously integrate multiple streams of data (including case, contact tracing, quarantine, mobility, mortality, testing and phylogenetic data), in order to fit outbreak trajectories and assess relative efficacies of the different control measures.

Multiple circulating strains of infectious disease pose dangers for public health, along with complex dynamics, underscoring recent and current research on dengue, cholera and nosocomial bacterial infections. For nosocomial infections, antibiotic resistant bacteria and environmental transmission in hospitals play a key role, along with stochasticity, which we model to assess impacts of control strategies such as health care worker hygeine. Current work is motivated by recent cholera outbreaks where cycling or switching of two serotypes, strains of the cholera bacteria that mainly differ in their induced host immunity. We combine and extend previously studied water transmission SIRW and multi-strain models to consider the strain diversity of cholera with environmental reservoir and characterize how persistence of coexisting strains manifests as serotype cycling.

The work on modeling COVID-19 is currently supported by NSF grant DMS 2028728

Selected Publications

• C. Browne, H. Gulbudak, & J. C. Macdonald (2022).Differential impacts of contact tracing and lockdowns on outbreak size in COVID-19 model applied to China. Journal of Theoretical Biology, 532, 110919.
• C. Browne, M. Wang, & G. F. Webb (2017). A Stochastic Model of Nosocomial Epidemics in Hospital Intensive Care Units. Electronic Journal of Qualitative Theory of Differential Equations, (6), 1-12
• C. Browne & G. F. Webb (2017). A Nosocomial Epidemic Model with Infection of Patients Due to Contaminated Rooms. Mathematical Biosciences and Engineering, 12(4), 761-787.
• G. Webb, C. Browne, X. Huo, O. Seydi, M. Seydi, & P. Magal (2015). A model of the 2014 ebola epidemic in west Africa with contact tracing. PLOS Currents, 7.