Research

My research focuses on (i) the analysis and application of systems of nonlinear ordinary and partial differential equations, (ii) the development of computational methods for solving multi-scale PDE models, and (iii) developing identifiability, sensitivity, and uncertainty analyses for multi-scale models to simultaneously fit data from several scales, in order to study host-pathogen ecology and evolution.

Multi-scale PDE models connecting immunology and epidemiology

A key challenge for disease modeling and public health is understanding pathogen dynamics across scales. COVID-19 and dengue epidemics are prime examples for the interdependence of population-level and individual-level dynamics through factors like immunity and vaccination. My specific areas of research include the development and analysis of multi-scale infectious disease models that include dynamics at the epidemiological and immunological scales and application to data rich systems. Unifying these scales requires novel structured PDE models, along with innovative analytical and computational developments to understand the model dynamics and apply them to biological data.

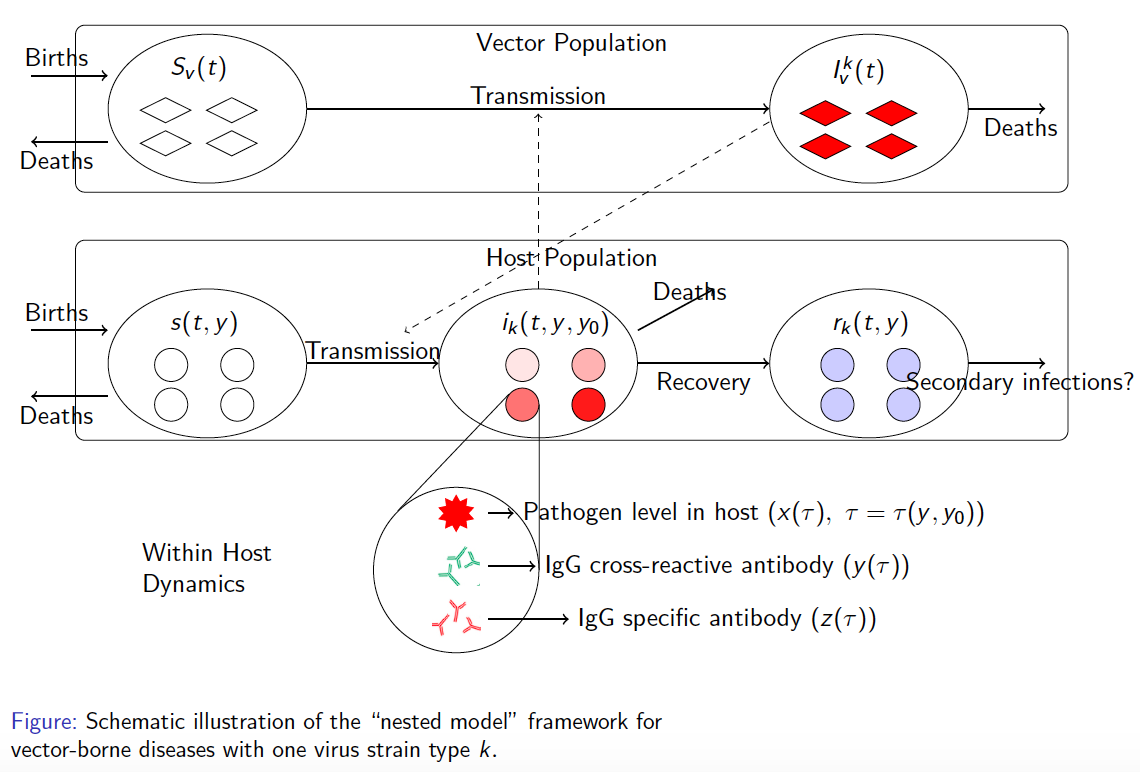
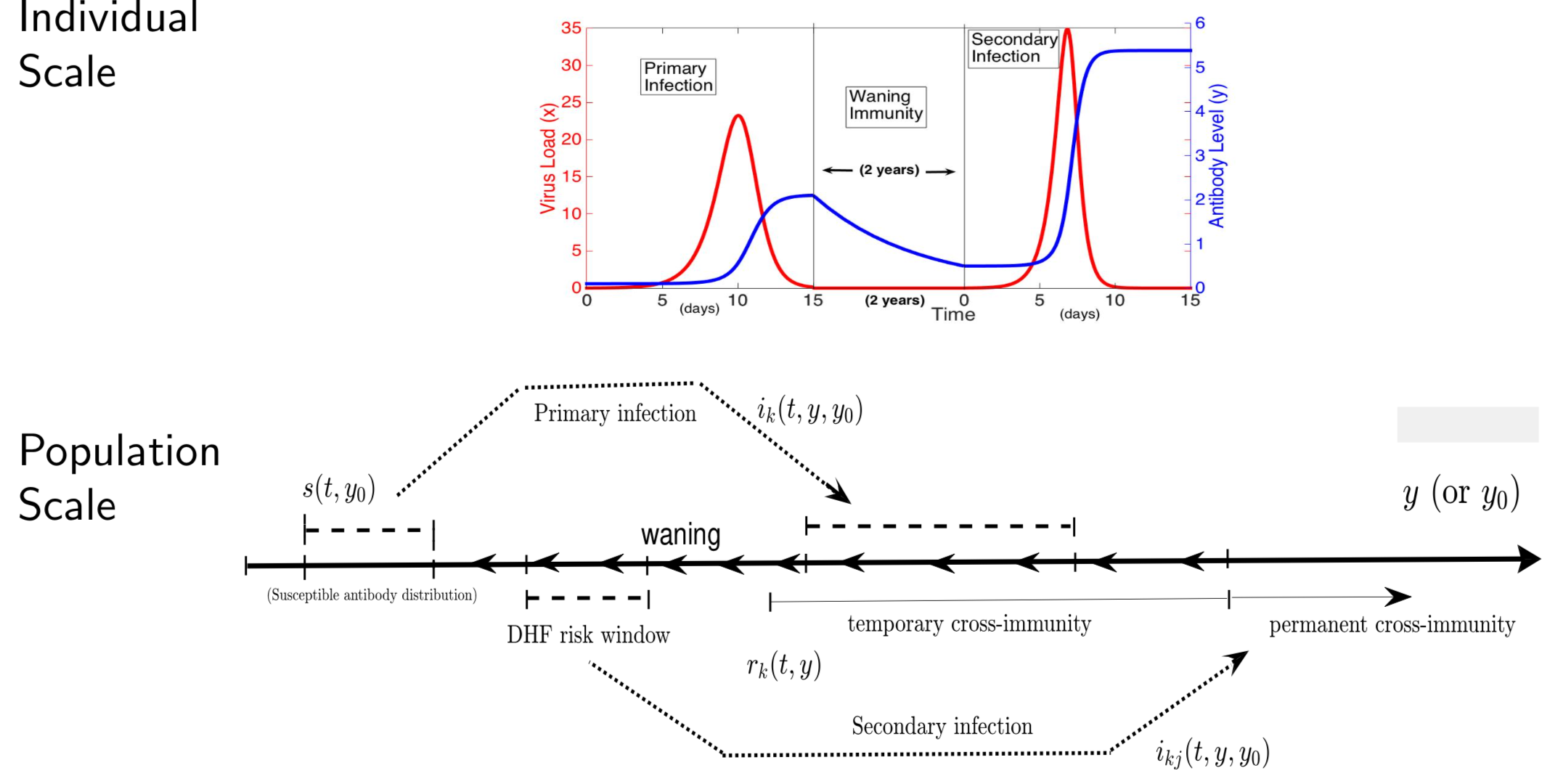
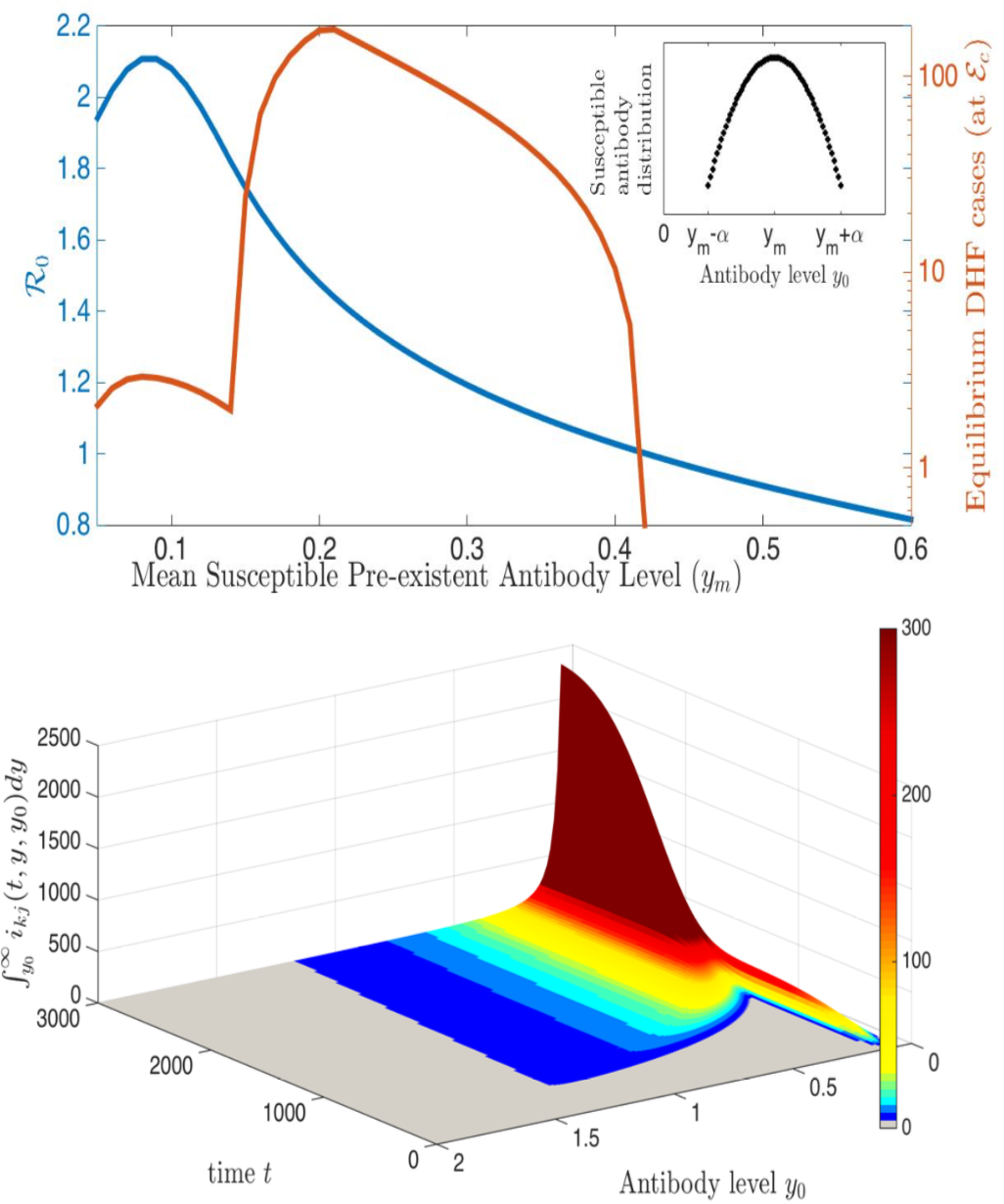
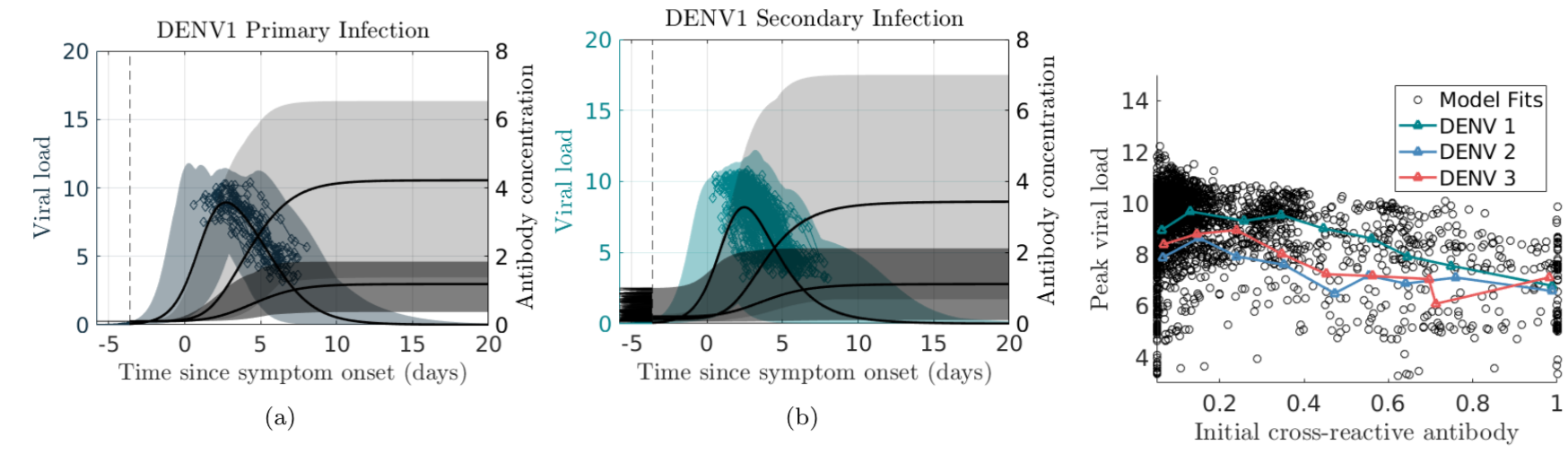
In the case of dengue, recent studies have shown severe infection is associated with intermediate levels of immunity due to a phenomenon called antibody dependent enhancement (ADE). In recent work, published in Journal of Mathematical Biology, we develop and analyze an innovative multi-scale immunological and antibody level structured multi-strain epidemic PDE model of dengue with ADE. The model tracks the infection on both scales by capturing the individual's dynamic state of immunity, via neutralizing antibody level within-the host, boosted through infection or vaccination and waning through time that are impacting individual and population level disease burden. The work includes novel stability results and multi-scale simulation techniques for the PDE model verified to converge to formulated equilibrium distributions. One important implication of the work is quantifying levels of vaccination in susceptible population that reduce or even ultimately eliminate dengue on population scale, but cause a rise in severe cases, increasing risk for individuals with certain antibody levels, motivating current work on extending model to include vaccination.

My other work on construction and dynamical systems analysis of multi-scale disease models include developing adaptive dynamics of host-pathogen coevolution trajectories in nested immuno-epidemiological ODE-PDE models for vectorborne diseases, and extension of models to include within-vector virus kinetics. Both topics highlight the power of unifying immunology and epidemiology in multi-scale models to understand the dynamics of evolving and complex pathogens, such as SARS-CoV-2 and dengue, motivating ongoing work.

This work has been supported by the NSF grant (DMS 1951759), and by the grant from the Simons Foundation. SFARI(638193)

Model fitting and inference with multi-scale data

An important scientific and mathematical problem for multi-scale modeling is fitting the models to data (i.e. parameter estimation) and incorporating data into model analysis and verification. My research has focused on developing computational techniques for the nested multi-scale PDE structured models, as above, along with helping to fill the gap for reliable methods such as identifiability analysis, parameter estimation and sensitivity analysis of immuno-epidemiological and other infectious disease models, which can be utilized to compare with data, infer impacts of parameter variability and provide accurate predictions.

Challenges to confronting multi-scale models with data include integrating mismatched observations across biological levels. For example, in current work on dengue multi-scale model fitting, we solve the ``data mismatch problem'' of primary and secondary infection data not being from the same patients or virus strain by a simultaneous weighted least squares minimization with sequential Monte Carlo statistical algorithm. My ongoing research focuses on adapting fitting, identifiability and sensitivity methods to multi-scale models and data for dengue, COVID-19, and Foot and Mouth Disease to understand viral evolution and dynamics at the cellular, within-host, population and landscape scales using experiments, observational field studies and phylogenetics.

For this project, I am collaborating with experimental and quantitative biologists from Oregon State University, the Pirbright Insitute (UK), Los Alamos Lab, and University of Warwick (UK), and the work is supported by a US-UK NSF collaboration grant DEB 2208087, along with DMS 1951759

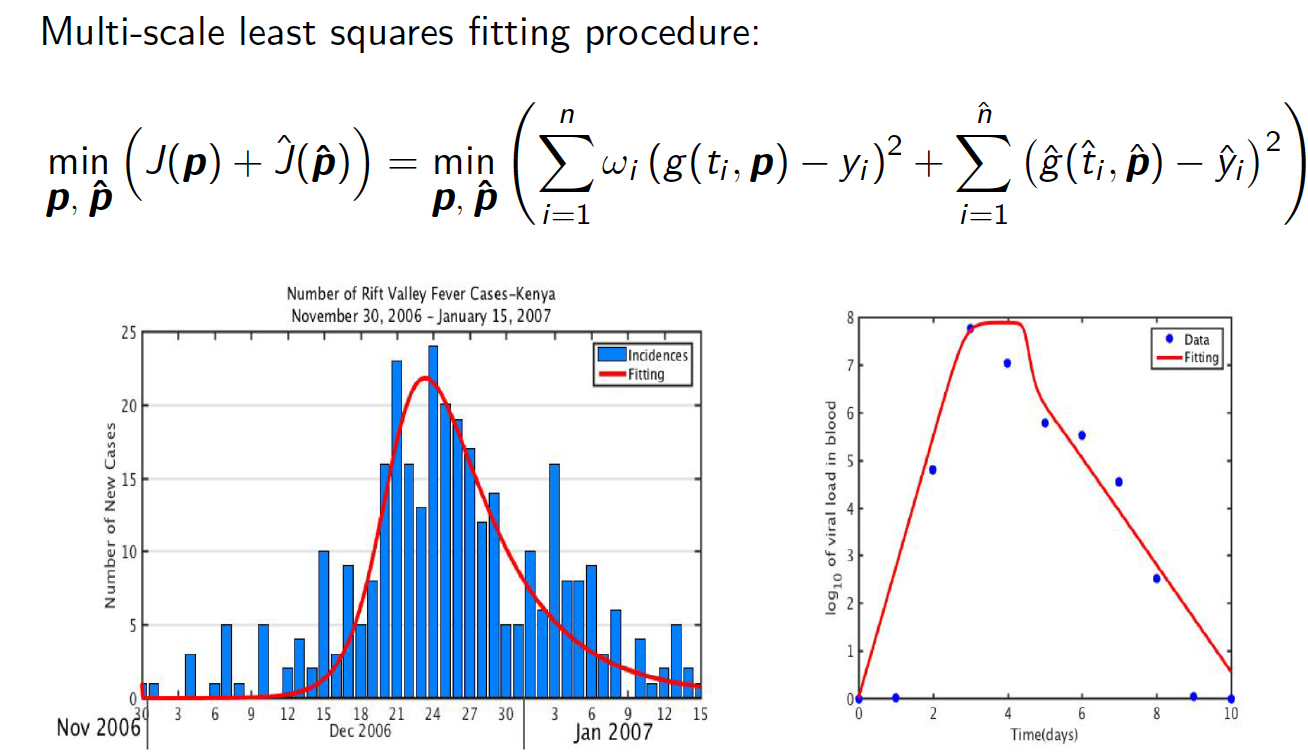
Modeling control strategies for infectious disease outbreaks

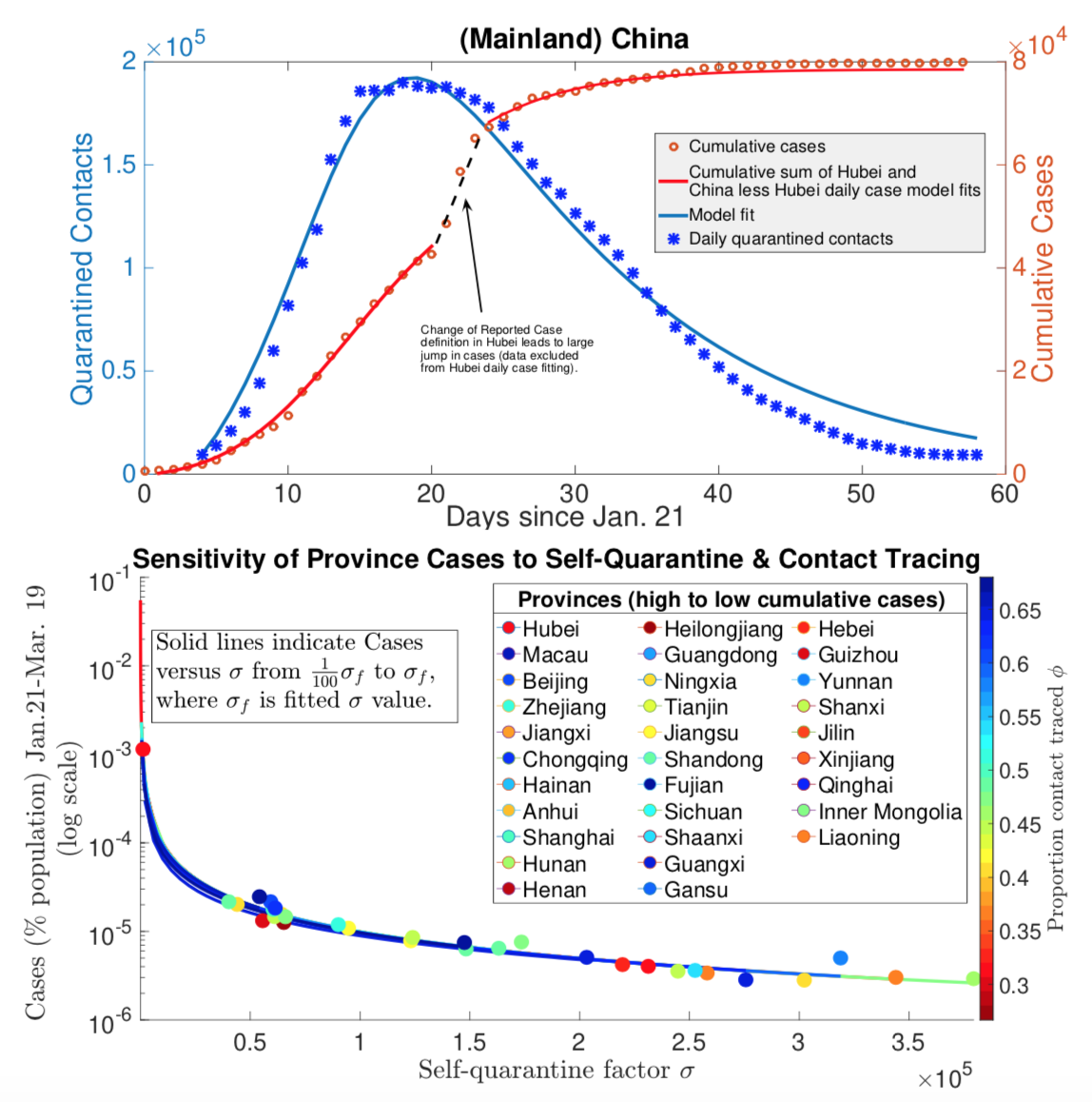
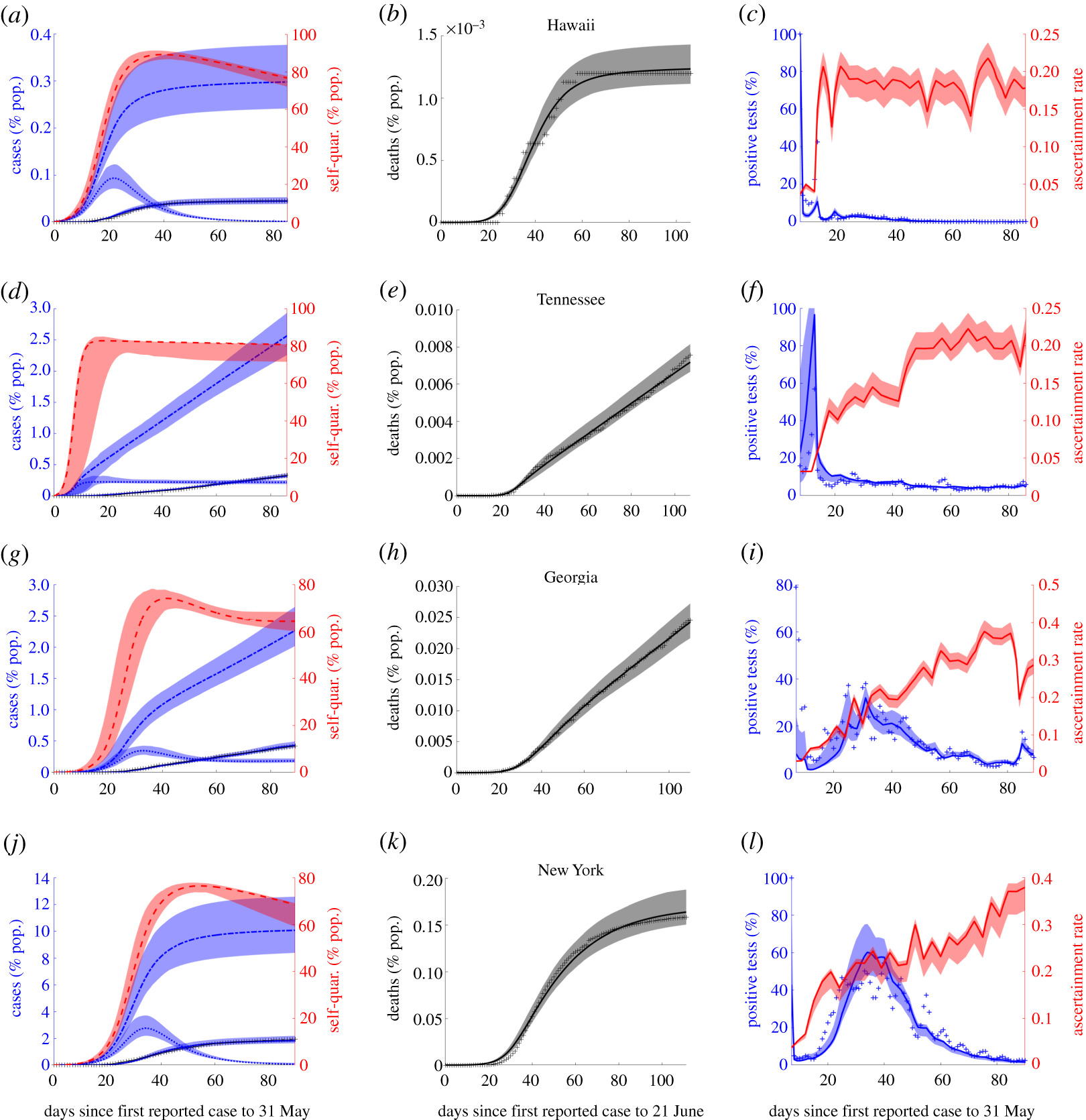
The COVID-19 pandemic illustrated the need for informed and efficient strategies for controlling and mitigating the spread of diseases. My prior work focuses on modeling the efficacy of contact tracing for Ebola epidemics and reactive culling for avian flu outbreaks in poultry. In more recently published papers in the Journal of Theoretical Biology and Royal Society Open Science, I and collaborators analyzed models incorporating vaccines, disease treatments, and contact-based interventions (contact tracing, quarantine and social distancing). In that work, we derived novel final size formulas consistent with fitting results using case, quarantine and testing data from Chinese provinces and U.S. states. Our results showed that lockdowns differentially compressed the Chinese and American outbreaks inversely proportional to quarantine rate, whereas contact tracing only reduced the peak with minimal impact on the final size.

This work has been supported by the NSF RAPID grant (DMS 1951759)

Bifurcation theory for virus & microbial host systems

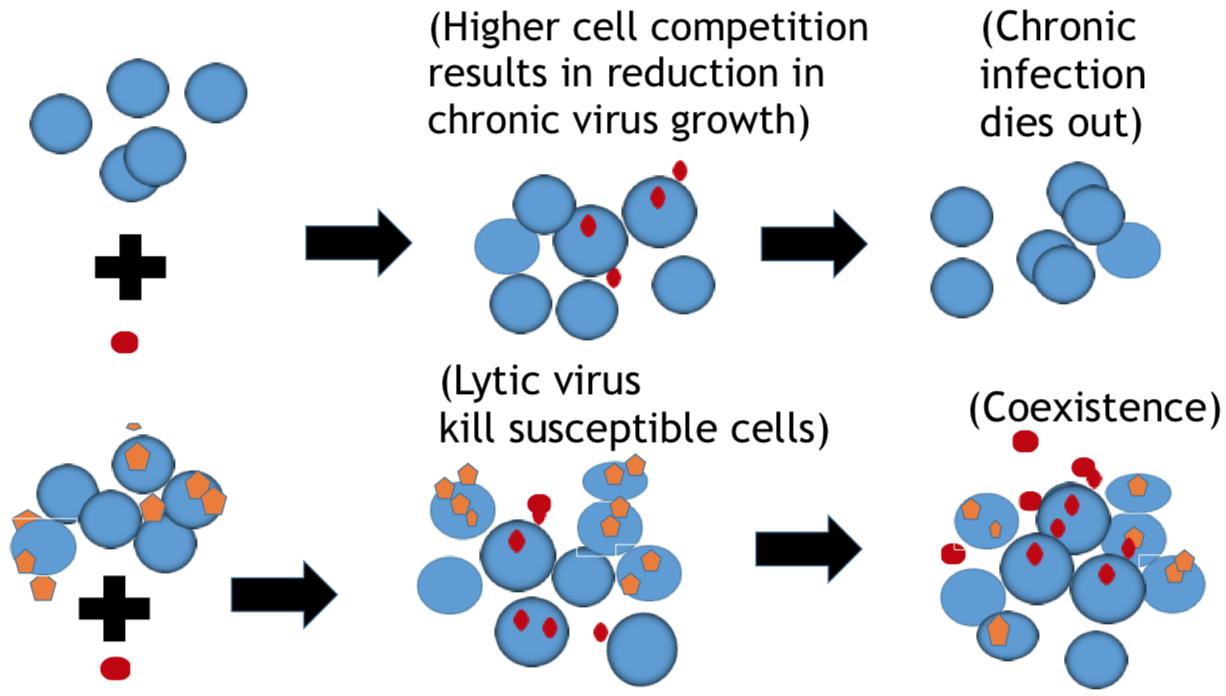
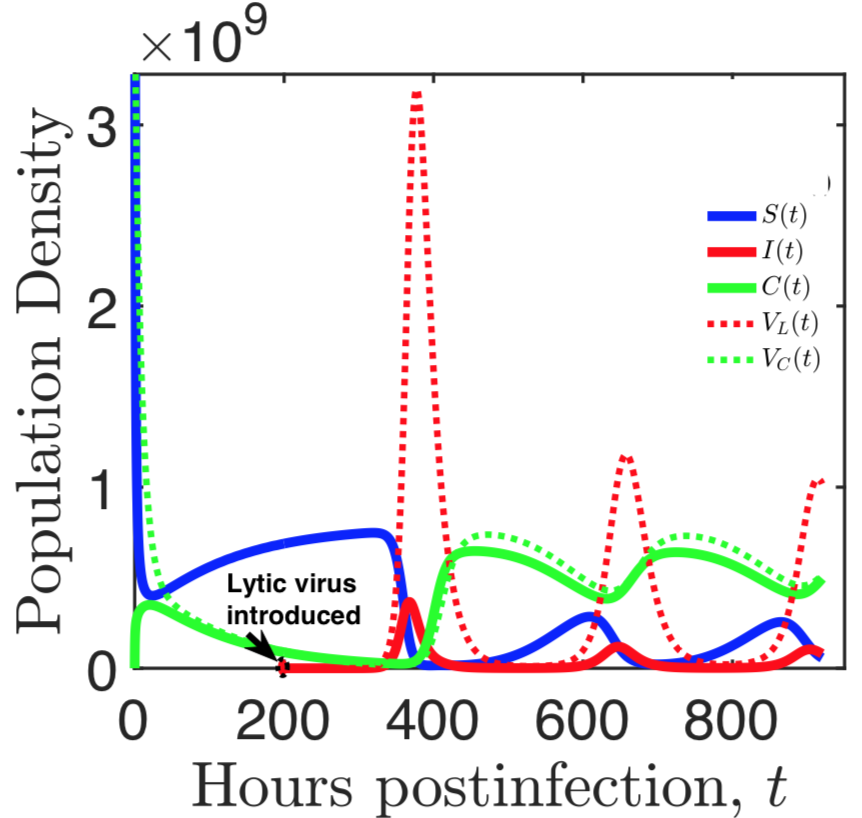
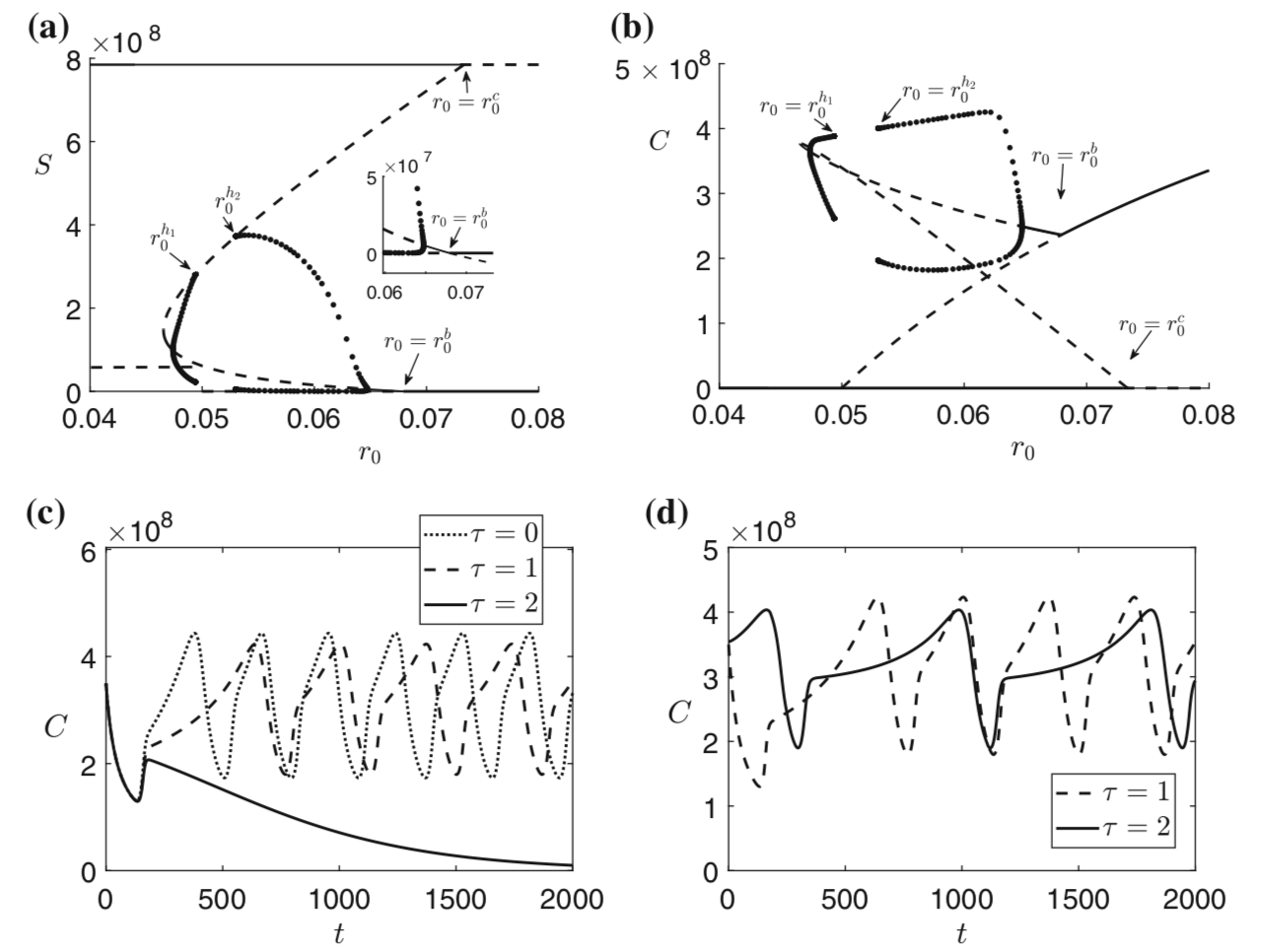
Bacteria and the viruses targeting them, called phages, are diverse and abundant, affecting the function of ecosystems and the health of hosts. Bacteria and phages also provide unparalleled opportunities for experimental study of co-evolutionary dynamics, and their outcomes for organismal traits and interactions. In my research, motivated by empirical studies, I use invasion analysis, bifurcation theory and adaptive dynamics approach along with computational methods to analyze nonlinear ODE and time delay models to investigate the ecology and evolution of viruses (phages) and their microbial hosts. For example, in a previous publication in Journal of Theoretical Biology I analyze viral replication strategy in a multi-species virus-microbe model, and, interestingly, find a regime in which the chronic virus requires the lytic virus for survival and invasion. This work is also extended for viral invasion fitness across a continuum from lysis to latency (published in the journal Virus evolution). In a recent article (published in Journal of Mathematical Biology), my collaborators and I extend the model by including explicit delay for eclipse stage of chronically infected cells and analyze persistence and bifurcations to obtain more insight on the survival of virus populations which can replicate by cell division and budding, such as non-virulent phage and HIV.