This is webpage about figures of constant width on a chessboard. I have written a paper about them with Janko Hernandez ( .pdf). Here I'll put some additional stuff that was left out of the paper. Also, here is an update on some of the questions mentioned below.

1. Figures of constant width on a chessboard.

We call figure a finite set of squares in a finite or infinite chessboard. Here is a figure forming a 3x3 square in an infinite chessboard.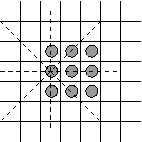

The row, column and diagonals passing through one of the squares of the figure are indicated with dashed lines. A familiar property of this figure is that every row or column of the chessboard that intersects it contains exactly 3 squares of the figure. We say that this figure has constant width 3 on rows and columns. We arrive to the following definition:

Definition. We shall say that a figure has constant width w if every row, column or diagonal of the chessboard that intersects the figure, intersects it in exactly w squares.

By a diagonal of the chessboard I mean the set of all squares with coordinates (i,j) such that i+j is constant or i-j is constant. For example, a single square in the corner of a finite chessboard forms a diagonal of the chessboard.

Here is the simplest figure of constant width 2: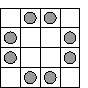

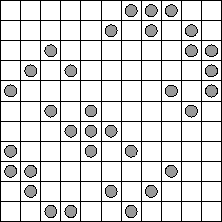
What about figures of width 3 or higher? Are there any?, and if so, are they easy to find? Yes there are many; but no, they are not so easy to find. In contrast with the figure of width 2 shown above, it seems that the smallest figure of width 3 contains 30 squares. Here it is

Let's make things more difficult and try and search for figures of constant width w, that fit inside a given chessboard of size nXn, and containing exactly kw squares. We shall say that such a figure is of type (n,k,w) .Thus, Figures 1 and 2 above are of type (4,4,2) and (11,10,3) respectively. The figures of type (n,n,1) are the solutions of the n-queens problem; that is, the configurations of n queens on an nXn chessboard such that they do not attack each other. They are known to exist for all n>=6 (see [Riv-Var-Zimm] ).

Theorem 1. (J. Hernandez, L. Robert). For every w there are constant width figures of type (n,k,w) for all pairs (n,k) with n>= k and k sufficiently large.

This theorem is proven by constructing some huge figures of constant width w. However, with the aid of a computer one can do better. We used an implementation of simulated annealing to find figures of width 3 and higher. Here are two figures of type (11,11,3) found with the computer:

These are some findings suggested by our computer searches. Since squeens does not do an exhaustive search we can not be sure of these statements.

1. Up to rotations and reflections, there is only one figure of type (11,10,3). There are no figures of type (n,k,3) for k<10 or n<11.
2. This list possibly exhausts all figures of type (12,10,3). They all look quite nice, only a few don't have some kind of symmetry. Here are some:
3. We have found figures of type (11,11,3), (14,14,4) and (17,17,5). If we had found a figure of type (20,20,6) I would dare to conjecture that there is a figure of type (3w+2,3w+2,w) for all w>0. But squeens didn't take us that far. So the question is:

   Question. Is there a figure of type (20,20,6)?

   It might also be that there are no figures of type (n,n,w) for n<3w+2. This is very likely for w<=4, as suggested by our computer searches.

2. The generating series.

Let us denote by W(n,k,w) the number of figures of type (n,k,w). The rotations and reflections of a figure are considered to be different unless the figure is left fixed by those transformations. We form the generating series

Theorem 2. R(k,w) is a rational function with denominator of the form .

For w=1 this theorem is an exercise in [Stan]. The proof for arbitrary w follows exactly the same technique.

3. Generalizations.

These are some obvious variations and generalizations of the problem. I haven't explored them much.